64. ročník matematickej olympiády 2014-2015
Súťažné úlohy kategórií Z5-Z9

aktualizované 8.4.2015 22:15

Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce
obvodné	obvodné	obvodné	obvodné	obvodné
				krajské
Zadania úloh domáceho kola na stiahnutie vo formáte PDF: (uložiť ako …)

Z5-I-1
Chlapci si medzi sebou menili známky, guľôčky a loptičky. Za 8 guľôčok je 10 známok, za 4 loptičky je 15 známok. Koľko guľôčok je za jednu loptičku?

Z5-I-2
Žabí princ sa zúčastnil skokanskej súťaže, pri ktorej sa skákalo po kameňoch rozmiestnených ako na obrázku. Bolo dovolené skákať len na najbližšie kamene východným alebo južným smerom. Každý skok na východ bol ocenený dvoma bodmi, každý skok na juh bol ocenený piatimi bodmi. Žabí princ získal 14 bodov. Určte všetky možné cesty, kadiaľ mohol skákať.

Z5-I-3
Z čísla 215 môžeme vytvoriť štvorciferné číslo tým, že medzi jeho cifry vpíšeme ďalšiu cifru. Takto sme vytvorili dve štvorciferné čísla, ktorých rozdiel bol 120. Aké dve štvorciferné čísla to mohli byť? Určte aspoň jedno riešenie.

Z5-I-4
Nájdite najväčšie číslo také, že

• žiadna cifra sa v ňom neopakuje,
• súčin každých dvoch cifier je nepárny,
• súčet všetkých cifier je párny.

Z5-I-5
Na obrázku je štvorec rozdelený na 25 štvorčekov. Vyfarbite štvorčeky piatimi farbami tak, aby platilo:

• každý štvorček je vyfarbený jednou farbou,
• v žiadnom riadku ani v žiadnom stĺpci nie sú dva štvorčeky rovnakej farby,
• na žiadnej z oboch uhlopriečok nie sú dva štvorčeky rovnakej farby,
• žiadne dva rovnako zafarbené štvorčeky sa nedotýkajú stranou ani vrcholom.

Z5-I-6
Na medaile, ktorá má tvar kruhu s priemerom 20 cm, je narysovaný snehuliak tak, že sú splnené nasledujúce požiadavky:

• snehuliak je zložený z troch kruhov ako na obrázku,
• priemery všetkých kruhov vyjadrené v cm sú celočíselné,
• priemer každého väčšieho kruhu je o 2 cm väčší ako priemer kruhu predchádzajúceho.

Určte výšku čo najväčšieho snehuliaka s uvedenými vlastnosťami.

Z5-II-1
V kúzelníckom bazáre si kúzelníci medzi sebou vymieňali kúzelnícke klobúky, paličky a plášte. Za 4 paličky je 6 plášťov a za 5 paličiek je 5 klobúkov. Koľko plášťov je za 5 paličiek a 1 klobúk?

Z5-II-2
Juro mal tri zhodné obdĺžniky. Najskôr ich k sebe priložil tak ako na obrázku a dostal obdĺžnik, ktorý mal obvod 20 cm. Potom ich k sebe priložil inak a dostal obdĺžnik s iným obvodom. Aký obvod mal tento obdĺžnik?

Z5-II-3
Z čísla 215 môžeme vytvoriť štvorciferné číslo tak, že medzi jeho cifry vpíšeme akúkoľvek ďalšiu cifru. Takto sme vytvorili dve štvorciferné čísla, ktorých súčet bol 4 360. Aké dve štvorciferné čísla to mohli byť? Určte všetky možnosti.

Z6-I-1
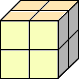
Erika a Peter dostali kocku, ktorá mala každú stenu rozdelenú na štyri rovnaké štvorce (pozri obrázok). Peter tvrdil, že sa dajú do všetkých štvorcov vpísať čísla 1 alebo 2 tak, aby na každej zo šiestich stien bol iný súčet. Erika naopak tvrdila, že to možné nie je. Rozhodnite, kto z nich mal pravdu.

Z6-I-2
Janíčko a Walter zbierali autíčka. Walter mal autíčka uložené v skrinke na troch poličkách. Najviac autíčok stálo na hornej poličke, na prostrednej ich bolo o tri menej ako na hornej a na spodnej poličke ich bolo o tri menej ako na prostrednej. Pritom na jednej z týchto poličiek bolo 15 autíčok. Keď si Janíčko zbierku prezrel, povedal Walterovi: „Myslel som si, že keď mám viac ako 20 autíčok, tak ich mám veľa. Teraz ale vidím, že ty máš dvakrát viac autíčok ako ja!“ Koľko autíčok mal vo svojej zbierke Janíčko?

Z6-I-3
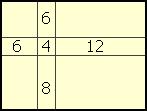
Pán Karfiól má obdĺžnikovú záhradu rozdelenú na 9 pravouholníkových záhonov ako na obrázku. Pri piatich záhonoch sú zapísané veľkosti ich obvodov v metroch. Určte obvod celej záhrady pána Karfióla.

Z6-I-4
Katka, Barbora a Adela sa dohadovali, ktoré dvojciferné číslo je najkrajšie. Katka vravela, že to je to jej, pretože je deliteľné štyrmi, a keď ho napíše pospiatky, dostane iné dvojciferné číslo, ktoré je tiež deliteľné štyrmi. Barbora tvrdila, že je to určite to jej, pretože jedna z jeho cifier je násobkom druhej. Adela o svojom obľúbenom čísle prezradila, že sa dá rozložiť na súčin štyroch prvočísel. Nakoniec kamarátky zistili, že hovoria všetky o tom istom čísle. Určte, ktoré číslo to bolo.

Z6-I-5
Určte, koľko rôznych riešení má nasledujúci algebrogram. Každé písmeno zodpovedá jednej cifre od 0 do 5, rôzne písmena zodpovedajú rôznym cifrám, rovnaké rovnakým.

K O S A
S A K O
B A B A

Z6-I-6
Skauti na výlete hrali hru. V lese bolo rozmiestnených 8 stanovísk prepojených špagátmi tak, ako na obrázku. Na každom stanovisku sa vydávalo jedno písmenko, prípadne pomlčka. Stanoviská sa dajú pozdĺž špagátov prebehnúť tak, že získané znaky tvoria reťazec

ANANAS-KOKOS-MANGO.

Priraďte jednotlivým stanoviskám zodpovedajúce znaky.

Z6-II-1
Fabián má štyri kartičky, na každú z nich napísal jedno celé kladné číslo menšie ako 10. Čísla napísal štyrmi rôznymi farbami, pričom platí:

• Súčin zeleného a žltého čísla je zelené číslo.
• Modré číslo je rovnaké ako červené číslo.
• Súčin červeného a modrého čísla je dvojciferné číslo zapísané zelenou a žltou cifrou (v tomto poradí).

Určte tieto štyri čísla.

Z6-II-2
Na deň detí otvorili v ZOO bludisko so šiestimi stanoviskami, na ktorých sa rozdávali cukríky. Na jednom stanovisku sa pri každom vstupe rozdávalo 5 cukríkov, na dvoch stanoviskách sa rozdávali 3 cukríky a na troch stanoviskách 1 cukrík. Juraj najskôr vstúpil na stanovisko označené na obrázku šípkou a pokračoval tak, že každou cestičkou prešiel nanajvýš raz. Určte, koľko najviac cukríkov mohol Juraj dostať.

Z6-II-3
Jano mal štyri zhodné trojuholníky. Skladal z nich rôzne útvary, a to tak, že trojuholníky k sebe prikladal stranami rovnakej dĺžky. Najskôr zložil útvar z troch trojuholníkov ako na obrázku 3a, ktorý mal obvod 43 cm. Potom útvar rozobral a zložil iný útvar z troch trojuholníkov, ktorý mal obvod 35 cm. Nakoniec zo všetkých štyroch trojuholníkov zložil ďalší útvar ako na obrázku 3b, a ten mal obvod 46 cm. Určte dĺžky strán trojuholníkov.

Z7-I-1
Ľuboš, Martin a ich kamarátka Erika šetria na hračku. Ľuboš a Martin prispeli do spoločnej pokladničky rovnakým množstvom eur, Erika prispela inou sumou. Keby Erika prispela len tretinou z toho, čo do pokladničky dodala, celkom by mali polovicu zo sumy, ktorá je v pokladničke teraz. Koľkokrát viac eur do pokladničky dodala Erika ako Ľuboš?

Z7-I-2
Lenka sa bavila tým, že vyťukávala na kalkulačke čísla. Používala iba cifry od 2 do 9 (pozri obrázok) a čoskoro si všimla, že niektoré zápisy boli osovo súmerné. Určte počet všetkých nanajvýš trojciferných čísel s uvedenými vlastnosťami.

Z7-I-3
Podľa projektu bude dno bazénu pokryté kamienkami troch farieb tak, ako ukazuje obrázok (dno je navyše rozdelené na 25 zhodných pomocných štvorcov). Cena kamienkov na jednotku plochy sa pri jednotlivých farbách líši. Projektant počítal cenu kamienkov použitých na takto pokryté dno a na jeho prekvapenie sa za každý druh kamienkov utratí rovnaká suma. Ďalej spočítal, že keby celú plochu pokryl tými najlacnejšími kamienkami, boli by náklady 1700€. Zistite, aké by boli náklady, keby celé dno nechal
pokryť tými najdrahšími kamienkami.

Z7-I-4
Body N, O, P a Q sú vzhľadom na trojuholník KLM zadané nasledujúcim spôsobom:

• Body N a O sú postupne stredy strán KM a KL,
• Vrchol M je stredom úsečky NP,
• Bod Q je priesečníkom priamok LM a OP.

Určte, aký je pomer dĺžok úsečiek MQ a ML.

Z7-I-5
Na starom hrade býva drak a väzní tam princeznú. Jano išiel princeznú oslobodiť, na hrade objavil troje dvier s nasledujúcimi nápismi.

  I: „Jaskyňa za dverami III je prázdna.“
II: „Princezná je v priestore za dverami I.“
III: „Pozor! Drak je v jaskyni za dverami II.“

Dobrá víla Janovi prezradila, že na dverách, za ktorými je princezná, je nápis pravdivý, pri drakovi je nepravdivý a na dverách prázdnej jaskyne môže byť napísaná pravda aj lož. Jano má na oslobodenie princeznej iba jeden pokus. Ktoré dvere má otvoriť?

Z7-I-6
Matej má dve kartičky, na každú z nich napísal jedno dvojciferné číslo. Ak zaradí menšie číslo za väčšie, dostane štvorciferné číslo, ktoré je deliteľné štyrmi a deviatimi. Ak zaradí naopak väčšie číslo za menšie, dostane štvorciferné číslo, ktoré je deliteľné piatimi a šiestimi. Koľko dvojíc kartičiek mohol Matej vyrobiť tak, aby platili vyššie uvedené podmienky? Určte všetky možnosti.

Z7-II-1
Nájdite všetky prirodzené čísla od 90 do 150 také, že ciferný súčet ich ciferného súčtu je rovný 1.

Z7-II-2
Siedme triedy z našej školy súťažili v zbieraní vrchnákov z PET fliaš. Trieda A nazbierala štvrtinu toho, čo triedy B a C dokopy, trieda B nazbierala pätinu toho, čo triedy A a C dokopy, a trieda C nazbierala 570 vrchnákov. Určte, koľko vrchnákov nazbierali tieto tri triedy spolu.

Z7-II-3
Prebieha rekonštrukcia námestia v tvare štvorca so stranou 20 metrov. Keby bolo celé vydláždené lacnejšou svetlou dlažbou, boli by náklady na materiál 10 000 €. Keby bolo celé námestie pokryté drahšou tmavou dlažbou, stál by materiál 30 000 €. Architekt však v centrálnej časti námestia navrhol svetlú štvorcovú časť, ktorá bude olemovaná pruhom tmavej dlažby o šírke 2 metre, a vo vonkajšej časti námestia bude rovnaká svetlá dlažba ako uprostred (pozri obrázok). Podľa tohto návrhu budú náklady na materiál tmavej časti rovnaké ako na celkový materiál svetlých častí. Určte:

• koľko stojí materiál na vydláždenie námestia podľa tohto projektu,
• aká dlhá je strana svetlého štvorca v centrálnej časti námestia.

Z8-I-1
Písmenkový logik je hra pre dvoch hráčov, ktorá má nasledujúce pravidlá:

1. Prvý hráč si myslí slovo zložené z piatich písmen, v ktorom sa žiadne písmeno neopakuje.
2. Druhý hráč napíše nejaké slovo z piatich písmen.
3. Prvý hráč odpovie dvoma číslami – prvé číslo udáva, koľko písmen napísaného slova sa zhoduje s mysleným slovom, t.j. stoja zároveň na správnom mieste, druhé číslo udáva, koľko písmen napísaného slova je obsiahnutých v myslenom slove, ale nestoja na správnom mieste.
4. Kroky 2 a 3 sa opakujú, kým druhý hráč myslené slovo neuhádne.

Záznam jednej hry dvoch kamarátov vyzeral nasledovne:

SONET	1	2
MUDRC	0	2
PLAST	0	2
KMOTR	0	4
ATOLY	1	1
DOGMA	0	2

V nasledujúcom ťahu bolo myslené slovo uhádnuté. Určte, ktoré slovo to bolo.

Z8-I-2
Súčet všetkých deliteľov istého nepárneho čísla je 78. Určte, aký je súčet všetkých deliteľov dvojnásobku tohto neznámeho čísla.

Z8-I-3
V lichobežníku KLMN platí, že

• strany KL a MN sú rovnobežné,
• úsečky KL a KM sú zhodné,
• úsečky KN, NM a ML sú navzájom zhodné.

Určte veľkosť uhla KNM.

Z8-I-4
Adam má plnú krabicu guľôčok, ktoré sú veľké alebo malé, čierne alebo biele. Pomer počtu veľkých a malých guľôčok je 5 : 3. Medzi veľkými guľôčkami je pomer počtu čiernych a bielych guľôčok 1 : 2, medzi malými guľôčkami je pomer počtu čiernych a bielych 1 : 8. Aký je pomer počtu všetkých čiernych a všetkých bielych guľôčok?

Z8-I-5
Priemer známok, ktoré mali na vysvedčení žiaci 8.A z matematiky, je presne 2,45. Ak by sme nepočítali jednotku a trojku súrodencov Michala a Aleny, ktorí do triedy prišli pred mesiacom, bol by priemer presne 2,5. Určte, koľko žiakov má 8.A.

Z8-I-6
Pejko dostal od svojho pána kváder zložený z navzájom rovnakých kociek cukru, ktorých bolo najmenej 1000 a nanajvýš 2000. Pejko kocky cukru odjedal po jednotlivých vrstvách – prvý deň odjedol jednu vrstvu spredu, druhý deň jednu vrstvu sprava a tretí deň jednu vrstvu zhora. Pritom v týchto troch vrstvách bol zakaždým rovnaký počet kociek. Zistite, koľko kociek mohol mať darovaný kváder. Určte všetky možnosti.

Z8-II-1
V rovnostrannom trojuholníku ABC leží na strane BC bod F. Obsah trojuholníka ABF je trikrát väčší ako obsah trojuholníka ACF a rozdiel obvodov týchto dvoch trojuholníkov je 5 cm. Určte dĺžku strany trojuholníka ABC.

Z8-II-2
Traja hudobníci Janek, Mikeš a Vávra si zvyčajne rozdelia spoločný honorár v pomere 4 : 5 : 6, najmenej dostane Janek a najviac Vávra. Tentoraz Vávra nehral dobre, a tak sa svojho podielu vzdal. Janek navrhol, že si Vávrovu časť rozdelia s Mikešom na polovice. Mikeš však trval na tom, aby si aj túto časť rozdelili nerovnomerne ako zvyčajne, teda v pomere 4 : 5. Mikeš by totiž podľa Jankovho návrhu dostal o 4 € menej ako podľa svojho. Určte výšku spoločného honorára.

Z8-II-3
Keď jeden rozmer kvádra zdvojnásobíme, druhý rozmer kvádra predelíme dvoma a tretí rozmer zväčšíme o 6 cm, dostaneme kocku, ktorá má rovnaký povrch ako pôvodný kváder. Určte rozmery tohto kvádra.

Z9-I-1
Milena nazbierala do košíka posledné spadnuté orechy a zavolala na partiu chlapcov, nech sa o ne podelia. Dala im ale podmienku: prvý si vezme 1 orech a desatinu zvyšku, druhý si vezme 2 orechy a desatinu nového zvyšku, tretí si vezme 3 orechy a desatinu ďalšieho zvyšku a tak ďalej. Takto sa podarilo rozobrať všetky orechy a pritom každý dostal rovnako veľa. Určte, koľko Milena nazbierala orechov a koľko sa o ne delilo chlapcov.

Z9-I-2
Lenka sa bavila tým, že vyťukávala na kalkulačke čísla, pričom používala iba cifry od 2 do 9 (pozri obrázok). Zápisy niektorých čísel mali tú vlastnosť, že ich obraz v osovej alebo stredovej súmernosti bol opäť zápisom nejakého čísla. Určte počet všetkých nanajvýš trojciferných čísel s uvedenými vlastnosťami.

Z9-I-3
Darček je zabalený do krabice, ktorej rozmery v cm sú 40×30×6. Krabica je previazaná špagátom ako na obrázku. Určte, koľko najmenej cm špagátu je treba na previazanie krabice, ak na uzol a mašľu stačí 20 cm.

Z9-I-4
Peter, Martin a Juro triafali do zvláštneho terča, ktorý mal iba tri políčka s hodnotami 12, 18 a 30 bodov. Všetci chlapci hádzali rovnakým počtom šípok, všetky šípky trafili do terča a výsledky každých dvoch chlapcov sa líšili v jedinom hode. Petrov priemerný bodový výsledok bol o dva body lepší ako Martinov a ten bol o jeden bod lepší ako priemer Jurov. Určte, koľkými šípkami hádzal každý z chlapcov.

Z9-I-5
Jaro si kúpil nové nohavice, ale boli príliš dlhé. Ich dĺžka bola vzhľadom k Jarovej výške v pomere 5 : 8. Mamička mu nohavice skrátila o 4 cm, čím sa pôvodný pomer zmenšil o 4 %. Určte, aký vysoký je Jaro.

Z9-I-6
Neznáme číslo je deliteľné práve tromi rôznymi prvočíslami. Keď tieto prvočísla zoradíme vzostupne, platí nasledujúce:

• Rozdiel druhého a prvého prvočísla je polovicou rozdielu tretieho a druhého prvočísla.
• Súčin rozdielu druhého a prvého prvočísla s rozdielom tretieho a druhého prvočísla je násobkom 17.

Určte najmenšie číslo, ktoré má všetky vyššie uvedené vlastnosti.

Z9-II-1
Myslím na niekoľko bezprostredne po sebe idúcich prirodzených čísel. Keby sme z nich vyškrtli čísla 70, 82 a 103, aritmetický priemer čísel by sa nezmenil. Keby sme namiesto toho vyškrtli čísla 122 a 123, aritmetický priemer by sa zmenšil presne o 1. Na ktoré prirodzené čísla myslím?

Z9-II-2
Po sebe idúce prirodzené čísla postupne pričítame a odčítame podľa nasledujúceho návodu:

Určte, aká bude hodnota takéhoto výrazu, ak jeho posledný člen je 2 015.

Z9-II-3
Anička dostala na narodeniny tortu v tvare obdĺžnika. Pomocou dvoch priamych rezov si odkrojila kúsok, ktorý je na obrázku vyznačený sivou. Určte, akú časť torty si Anička odkrojila.

Z9-II-4
Istý obdĺžnik mal svoje rozmery vyjadrené v decimetroch celými číslami. Potom rozmery trikrát zmenil. Najskôr jeden svoj rozmer zdvojnásobil a druhý zmenil tak, aby mal rovnaký obsah ako na začiatku. Potom jeden rozmer zväčšil o 1 dm a druhý zmenšil o 4 dm, pričom mal stále taký istý obsah ako na začiatku. Nakoniec svoj kratší rozmer zmenšil o 1 dm, dlhší ponechal bezo zmeny. Určte pomer strán posledného obdĺžnika.

Z9-III-1
Peter, Martin a Juraj triafali do zvláštneho terča, ktorý mal iba tri políčka s navzájom rôznymi hodnotami. Každý z chlapcov hádzal celkom desaťkrát a vždy trafil do terča. Bodový zisk z prvých ôsmich hodov mali všetci traja chlapci rovnaký. Pri posledných dvoch hodoch trafil Juraj dvakrát políčko s najnižšou možnou hodnotou, Martin dvakrát políčko so strednou hodnotou a Peter dvakrát políčko s najvyššou hodnotou. Aritmetický priemer všetkých Martinových hodov bol o 1 väčší ako Jurajov priemer a Petrov priemer bol o 1 väčší ako Martinov priemer. Určte všetky možné hodnoty políčok na terči, ak viete, že jedna z nich bola 12.

Z9-III-2
V trojuholníku ABC ležia na strane AB body E a F. Obsah trojuholníka AEC je 1 cm², obsah trojuholníka EFC je 3 cm² a obsah trojuholníka FBC je 2 cm². Bod T je ťažiskom trojuholníka AFC a bod G je priesečníkom priamok CT a AB. Bod R je ťažiskom trojuholníka EBC a bod H je priesečníkom priamok CR a AB. Určte obsah trojuholníka GHC.

Z9-III-3
Určte, aká je posledná cifra súčinu všetkých párnych prirodzených čísel, ktoré sú menšie ako 100 a ktoré nie sú násobkami 10.

Z9-III-4
Daný je obdĺžnik ABCD, ktorého kratšia strana je AB. Určte, pre ktoré body P na priamke AD platí, že os uhla BPD prechádza bodom C. Svoje tvrdenie zdôvodnite a popíšte, ako by ste všetky také body zostrojili.