66. ročník matematickej olympiády 2016-2017
Súťažné úlohy kategórií Z5-Z9

aktualizované 4.7.2017 14:45

Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce
obvodné	obvodné	obvodné	obvodné	obvodné
				krajské
Zadania úloh domáceho kola na stiahnutie vo formáte PDF: (uložiť ako …)

Z5-I-1
Zvonkohra na nádvorí hrá o každej celej hodine krátku skladbu, a to počínajúc 8. a končiac 22. hodinou. Skladieb je celkom osemnásť, o celej hodine sa hrá vždy iba jedna a po odohraní všetkých osemnástich sa začína v rovnakom poradí znova. Oľga a Ľuboš boli na nádvorí v pondelok o 15. hodine. Ten istý týždeň si prišli zvonkohru vypočuť ešte raz na poludnie, na ich sklamanie však hrala tá istá melódia, ktorú počuli v pondelok. Ktorý deň bola Oľga s Ľubošom na nádvorí druhý raz?

Z5-I-2
V každom z rohových políčok vonkajšieho štvorca má byť napísané jedno z čísel 2, 4, 6 a 8, pričom v rôznych políčkach majú byť rôzne čísla. V štyroch políčkach vnútorného štvorca majú byť súčiny čísel zo susediacich políčok vonkajšieho štvorca. V kruhu má byť súčet čísel zo susediacich políčok vnútorného štvorca. Ktoré čísla môžu byť napísané v kruhu? Určte všetky možnosti.

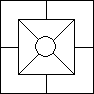
Z5-I-3
Na obrázku je štvorcová dlaždica so stranou dĺžky 10 dm, ktorá je zložená zo štyroch zhodných obdĺžnikov a malého štvorca. Obvod malého štvorca je päťkrát menší ako obvod celej dlaždice. Určte rozmery obdĺžnikov.

Z5-I-4
Predavač vianočných stromčekov predával smriečky po 22€, borovičky po 25€ a jedličky po 33€. Ráno mal rovnaký počet smriečkov, jedličiek a borovíc. Večer mal všetky stromčeky predané a celkom za ne utŕžil 3 600€. Koľko stromčekov v ten deň predavač predal?

Z5-I-5
Napíšte namiesto hviezdičiek cifry tak, aby súčet doplnených cifer bol nepárny a aby platila uvedená rovnosť:

Z5-I-6
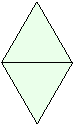
Jarka zostrojila dva zhodné rovnostranné trojuholníky ako na obrázku. Ďalej chce zostrojiť všetky kružnice, ktoré budú mať stred v niektorom z vrcholov a budú prechádzať niektorým iným vrcholom niektorého z trojuholníkov. Zostrojte a spočítajte všetky kružnice vyhovujúce Jarkiným požiadavkám.

Z5-II-1
Otec hral so strýkom šachy. Za vyhranú partiu dostal víťaz od súpera 8 eur, za remízu nikto nič. Strýko vyhral štyrikrát, remíz bolo päť a otec nakoniec získal 24 eur. Koľko partií otec so strýkom zohrali?

Z5-II-2
Veverička Hryzka ujedala oriešky zo svojich zásob nasledujúcim spôsobom:

• v diétny deň zjedla jeden oriešok,
• v normálny deň zjedla o dva oriešky viac ako v diétny deň.

Istých 19 po sebe idúcich dní sa striedali dni diétne s dňami normálnymi. Zistite, koľko najviac a koľko najmenej orieškov mohla Hryzka počas týchto 19 dní zjesť. 

Z5-II-3
Ema chce zostrojiť trojuholník ABC so stranami |AB| = 3 cm a |BC| = 4 cm. Ďalej chce zostrojiť všetky kružnice, z ktorých každá bude mať stred v niektorom z vrcholov trojuholníka a bude prechádzať niektorým jeho iným vrcholom. Aká dlhá musí byť strana AC, aby takých kružníc bolo práve päť?

Z6-I-1
Jana a Dávid trénujú sčítanie desatinných čísel tak, že každý z nich napíše jedno číslo, a tieto dve čísla potom sčítajú. Posledný príklad im vyšiel 11,11. Dávidovo číslo malo pred desatinnou čiarkou rovnaký počet cifier ako za ňou, Janino číslo tiež. Dávidovo číslo bolo zapísané navzájom rôznymi ciframi, Janino číslo malo práve dve cifry rovnaké. Určte najväčšie možné číslo, ktoré mohol napísať Dávid.

Z6-I-2
Pán Kockorád vlastnil záhradu obdĺžnikového tvaru, na ktorej postupne dláždil chodníky z jednej strany na druhú. Chodníky boli rovnako široké, križovali sa na dvoch miestach a už vydláždená plocha sa pri ďalšom dláždení preskakovala. Keď pán Kockorád vydláždil chodník rovnobežný s dlhšou stranou, spotreboval 228 m² dlažby. Potom vydláždil chodník rovnobežný s kratšou stranou a spotreboval 117 m² dlažby. Nakoniec vydláždil ešte jeden chodník rovnobežný s prvým chodníkom, tentoraz spotreboval len 219 m² dlažby. Určte rozmery Kockorádovej záhrady.

Z6-I-3
Mnohonožka Mirka pozostáva z hlavy a niekoľkých článkov, na každom článku má jeden pár nôh. Keď sa ochladilo, rozhodla sa, že sa oblečie. Preto si na treťom článku od konca a potom na každom ďalšom treťom článku obliekla ponožku na ľavú nôžku. Podobne si na piatom článku od konca a potom na každom ďalšom piatom článku obliekla ponožku na pravú nôžku. Napokon zistila, že na 14 článkoch jej zostali obe nohy bosé. Zistite, koľko celkom nôh mohla mať mnohonožka Mirka; určte všetky možnosti.

Z6-I-4
Štyri rodiny boli na spoločnom výlete. V prvej rodine boli traja súrodenci, a to Alica, Betka a Cyril. V druhej rodine boli štyria súrodenci, a to Dávid, Erika, Filipa Gabika. V tretej rodine boli dvaja súrodenci, a to Hugo a Iveta. Vo štvrtej rodine boli traja súrodenci, a to Ján, Karol a Lukáš. Cestou sa deti rozdelili na skupiny tak, že v každej skupine boli všetky deti s rovnakým počtom bratov a nikto iný. Ako sa mohli deti rozdeliť? Určte všetky možnosti.

Z6-I-5
Juro si nakreslil štvorcovú sieť s 25 štvorčekmi ako na obrázku. Potom chcel každý štvorček vyfarbiť tak, aby rovnako vyfarbené štvorčeky nemali spoločný žiadny vrchol. Koľko najmenej farieb musel Juro použiť?

Z6-I-6
Do prázdnych políčok v nasledujúcom obrázku doplňte celé čísla väčšie ako 1 tak, aby v každom tmavšom políčku bol súčin čísel zo susedných svetlejších políčok.

Z6-II-1
Na lúke sa zišli dve rodiny s celkom šiestimi deťmi, ktoré boli staré 2, 3, 4, 5, 6 a 8 rokov. Súčet vekov detí z jednej rodiny bol rovnaký ako súčet vekov detí z druhej rodiny. Aké staré mohli byť deti z každej rodiny? Určte všetky možnosti.

Z6-II-2
Pat a Mat kopali studňu. Prvý deň vykopal Pat jamu hlbokú 40 cm. Druhý deň pokračoval Mat a dokopal sa do trojnásobnej hĺbky. Tretí deň vykopal Pat toľko, koľko predchádzajúci deň vykopal Mat, a narazil na vodu. V tom okamihu bol povrch zeme 50 cm nad vrchom jeho hlavy. Určte, koľko cm meral Pat.

Z6-II-3
Traja záhradkári si pozvali oráča, aby im zoral ich pozemky. Oráč účtoval za každý zoraný meter štvorcový všetkým rovnakú cenu. Dokopy záhradkári zaplatili 57 €. Dva z pozemkov boli štvorcové, jeden bol obdĺžnikový. Plošný obsah obdĺžnikového pozemku bol 6 árov a jedna jeho strana merala 20 m. Dĺžka strany jedného štvorcového pozemku bola rovnaká ako dĺžka obdĺžnikového pozemku, dĺžka strany druhého štvorcového pozemku bola rovnaká ako šírka obdĺžnikového pozemku. Koľko zaplatil za zoranie každý zo záhradkárov?

Z7-I-1
Štvorec so stranou 4 cm je rozdelený na štvorčeky so stranou 1 cm ako na obrázku. Rozdeľte štvorec pozdĺž vyznačených čiar na dva útvary s obvodom 16 cm. Nájdite aspoň tri rôzne riešenia (tzn. také tri riešenia, aby žiadny útvar jedného riešenia nebol zhodný so žiadnym útvarom iného riešenia).

Z7-I-2
Na lyžiarske sústredenie prišli 4 kamaráti zo 4 svetových strán a viedli nasledujúci rozhovor.
      Karol: „Neprišiel som zo severu ani z juhu.“
      Mojmír: „Zato ja som prišiel z juhu.“
      Jozef: „Prišiel som zo severu.“
      Zdeno: „Ja som z juhu neprišiel.“
      Vieme, že jedna výpoveď nie je pravdivá. Určte, ktorá to je. Kto teda prišiel zo severu a kto z juhu?

Z7-I-3
Anička má 5€, Anežka má 4,60€ a za všetky peniaze chcú kúpiť zákusky na rodinnú oslavu. Rozhodujú sa medzi tortičkami a veterníkmi: veterník je o 0,40€ drahší ako tortička a tortičiek by sa dalo za všetky peniaze kúpiť o tretinu viac ako veterníkov. Koľko stojí každý zo zákuskov?

Z7-I-4
Napíšte namiesto hviezdičiek cifry tak, aby nasledujúci zápis súčinu dvoch čísel bol platný:

			*	*	*
	.		*	*	*
		*	*	*	*
	4	9	4	9
	*	*	*
*	*	*	4	*	*

Z7-I-5
Daný je trojuholník ABC so stranami |AB|= 3 cm, |BC|= 10 cm a s uhlom ABC o veľkosti 120°. Narysujte všetky body X také, aby platilo, že trojuholník BCX je rovnoramenný a súčasne trojuholník ABX je rovnoramenný so základňou AB.

Z7-I-6
Určte, pre koľko prirodzených čísel väčších ako 900 a menších ako 1 001 platí, že ciferný súčet ciferného súčtu ich ciferného súčtu je rovný 1.

Z7-II-1
Marienka dostala od babičky zázračný mešec, ktorý vždy cez noc zdvojnásoboval množstvo dukátov, ktoré obsahoval. V pondelok Marienka vložila do prázdneho mešca nejaké dukáty. V utorok a v stredu si z mešca vybrala vždy 40 dukátov a nič do neho nevkladala. Vo štvrtok si opäť vybrala 40 dukátov a mešec zostal prázdny. Koľko dukátov vložila Marienka v pondelok do mešca? Koľko dukátov mala do prázdneho mešca vložiť, aby mohla opakovane každý deň vyberať 40 dukátov, nemusela nič vkladať a aby každý deň pred výberom bol počet dukátov v mešci rovnaký?

Z7-II-2
Mriežka s deviatimi políčkami ako na obrázku je vyplnená deviatimi bezprostredne po sebe idúcimi prirodzenými číslami. Tie sú zoradené podľa veľkosti zľava doprava a zhora nadol (t. j. najmenšie číslo je vľavo hore, najväčšie je vpravo dole). Tučná lomená čiara rozdeľuje mriežku na dve časti. Súčet čísel v ľavej časti je o 100 menší ako súčet čísel v pravej. Ktoré číslo je v prostrednom políčku?

Z7-II-3
Adam má dva kvádre s objemami 12 cm³ a 30 cm³, pričom rozmery každého z nich sú v centimetroch vyjadrené navzájom rôznymi celými číslami. Adam zistil, že kvádre sa dajú zlepiť k sebe tak, aby lepené steny splývali, a získať tak nový kváder. Aké rozmery môže mať nový kváder? Určte všetky možnosti.

Z8-I-1
Tri kamarátky veveričky spolu vyrazili na zber lieskových orieškov. Ryšavka ich našla dvakrát viac ako Pizizubka a Uška dokonca trikrát viac ako Pizizubka. Cestou domov sa zhovárali a pritom lúskali a jedli svoje oriešky. Pizizubka zjedla polovicu všetkých orieškov, ktoré nazbierala, Ryšavka tretinu všetkých svojich orieškov a Uška štvrtinu tých svojich. Doma veveričky zistili, že im dokopy zvýšilo 196 orieškov. Koľko orieškov našla každá z veveričiek?

Z8-I-2
Na každej stene pravidelného osemstena je napísané jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, pričom na rôznych stenách sú rôzne čísla. Pre každú stenu Jaro určil súčet čísla na nej napísaného s číslami troch susedných stien. Takto dostal osem súčtov, ktoré tiež sčítal. Aké hodnoty môže tento výsledný súčet nadobúdať?

Z8-I-3
Pri streľbe z luku sa okrem iného sleduje výkonnosť strelca. Tá sa počíta tak, že sa zo všetkých pokusov odoberie jeden najlepší a jeden najhorší a z hodnotenia zvyšných sa spočíta aritmetický priemer. Kamaráti Peter, Juraj, Michal a Zdeno strieľali po jednom šípe v štyroch kolách. Každá strela bola hodnotená celým číslom od 0 do 10. V každom kole bol súčet hodnotení všetkých chlapcov 32 bodov, ale ani v jednom kole nemali žiadni dvaja chlapci rovnaké hodnotenie. V nasledujúcej tabuľke sú vyplnené iba niektoré údaje z uvedeného zápasu, doplňte tie chýbajúce.

	1. kolo	2. kolo	3. kolo	4. kolo	výkonnosť
Peter				5	10
Juraj			9	10	7,5
Michal			5		8
Zdeno					8,5
celkom	32	32	32	32	–

Z8-I-4
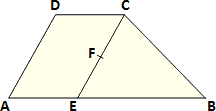
Lichobežník ABCD je úsečkou CE rozdelený na trojuholník a rovnobežník, pozri obrázok. Bod F je stredom úsečky CE, priamka DF prechádza stredom úsečky BE a obsah trojuholníka CDE je 3 cm². Určte obsah lichobežníka ABCD.

Z8-I-5
Mamička doniesla 10 zákuskov troch druhov: kokosiek bolo menej ako laskoniek a najviac bolo karamelových kociek. Jozef si vybral dva zákusky rôznych druhov, Jakub urobil to isté a na Jána zvýšili iba zákusky rovnakého druhu. Koľko kokosiek, laskoniek a karamelových kociek mamička doniesla?

Z8-I-6
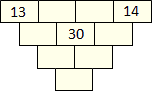
Každá tehlička nasledujúcej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo na nej. Ktoré číslo môže byť v najspodnejšej tehličke? Určte všetky možnosti.

Z8-II-1
Monika premýšľa o štvorcifernom čísle, ktoré má nasledujúce vlastnosti:

• súčin dvoch krajných cifier je 40,
• súčin dvoch vnútorných cifier je 18,
• rozdiel dvoch krajných cifier je rovnaký ako rozdiel dvoch vnútorných cifier,
• rozdiel mysleného čísla a opačne napísaného čísla (t. j. čísla napísaného rovnakými ciframi, ale v opačnom poradí) je najväčší možný.

Určte Monikino myslené číslo.

Z8-II-2
Mat kopal jamu. Pat sa ho spýtal, aká bude jama hlboká. Mat odpovedal hádankou:

„Meriam 90 cm a práve mám vykopanú polovicu jamy. Keď vykopem jamu celú, bude vrch mojej hlavy pod povrchom zeme tak hlboko, ako je teraz nad povrchom zeme.“

Akú hlbokú jamu Mat kopal?

Z8-II-3
Pravouhlý trojuholník ABC má odvesny |AB|= 5 cm a |BC|= 12 cm. Vrcholy trojuholníka ABC sú zobrazené tak, že

• bod A sa zobrazuje do bodu A‘ súmerne podľa osi uhla ABC,
• bod B sa zobrazuje do bodu B‘ súmerne podľa stredu úsečky BC,
• bod C sa zobrazuje do bodu C‘ súmerne podľa osi úsečky AB.

Určte obsah trojuholníka A’B’C. 

Z9-I-1
Vo všetkých deviatich políčkach útvaru majú byť vyplnené prirodzené čísla tak, aby platilo:

• každé z čísel 2, 4, 6 a 8 je použité aspoň raz,
• štyri políčka vnútorného štvorca obsahujú súčiny čísel zo susediacich políčok vonkajšieho štvorca,
• v kruhu je súčet čísel zo susediacich políčok vnútorného štvorca.

Zistite, ktoré najmenšie a ktoré najväčšie číslo môže byť napísané v kruhu.

Z9-I-2
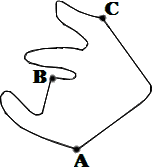
Z bodu A do bodu C vedie náučný chodník prechádzajúci bodom B a inakadiaľ tiež červená turistická značka, pozri obrázok. Okrem toho sa dá použiť aj nezakreslená skratka dlhá 1 500metrov začínajúca v A a ústiaca na náučnom chodníku. Vojtech zistil, že výlet z A po červenej do C a po náučnom chodníku späť do A je dlhý 7 700 metrov, výlet z B po náučnom chodníku do C a potom po červenej do A je dlhý 5 800 metrov, s využitím skratky je cesta z A do B dlhá 1 700 metrov, výlet z A po náučnom chodníku do C a späť do A najskôr po náučnom chodníku a potom po skratke je dlhý 8 800 metrov. Určte dĺžku náučného chodníka z A do C. Pokiaľ zadanie pripúšťa viac odpovedí, uveďte všetky.

Z9-I-3
Júlii sa zakotúľala loptička do bazéna a plávala vo vode. Jej najvyšší bod bol 2 cm nad hladinou. Priemer kružnice, ktorú vyznačila hladina vody na povrchu loptičky, bol 8 cm. Určte priemer Júliinej loptičky.

Z9-I-4
Katka si myslela päťciferné prirodzené číslo. Do zošita napísala na prvý riadok súčet mysleného čísla a polovice mysleného čísla. Na druhý riadok napísala súčet mysleného čísla a pätiny mysleného čísla. Na tretí riadok napísala súčet mysleného čísla a devätiny mysleného čísla. Nakoniec sčítala všetky tri zapísané čísla a výsledok napísala na štvrtý riadok. Potom s úžasom zistila, že na štvrtom riadku má zapísanú tretiu mocninu istého prirodzeného čísla. Určte najmenšie číslo, ktoré si Katka mohla myslieť na začiatku.

Z9-I-5
Myšky si postavili podzemný domček pozostávajúci z komôrok a tunelčekov:

• každý tunelček vedie z komôrky do komôrky (tzn. žiadny nie je slepý),
• z každej komôrky vedú práve tri tunelčeky do troch rôznych komôrok,
• z každej komôrky sa dá tunelčekmi dostať do ktorejkoľvek inej komôrky,
• v domčeku je práve jeden tunelček taký, že jeho zasypaním sa domček rozdelí na dve oddelené časti.

Koľko najmenej komôrok mohol mať myší domček? Načrtnite, ako mohli byť komôrky pospájané.

Z9-I-6
Daná je úsečka AB dĺžky 12 cm, na ktorej je jednou stranou položený štvorec MRAK so stranou dĺžky 2 cm, pozri obrázok. MRAK sa postupne preklápa po úsečke AB, pričom bod R zanecháva na papieri stopu. Narysujte celú stopu bodu R, kým štvorec neobíde úsečku AB z oboch strán a nevráti sa do svojej pôvodnej polohy.

Z9-II-1
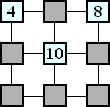
Do prázdnych políčok doplňte čísla tak, aby v políčkach uprostred každej vyznačenej
úsečky bol súčet čísel z jej krajných políčok a aby súčty čísel z políčok na oboch uhlopriečkach boli rovnaké.

Z9-II-2
Pat sčítal všetky štvorciferné čísla, z ktorých každé obsahovalo všetky cifry 1, 2, 3 a 4, a dospel k súčtu 58 126. Mat mu potvrdil, že počítal správne, ale že zabudol pripočítať dve z uvažovaných čísel. Zistite, na ktoré čísla Pat zabudol.

Z9-II-3
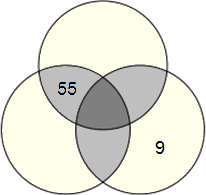
Vedci púšťali do bludiska potkany a sledovali, či sa dostanú do cieľa. Zistili, že čiernych potkanov došlo do cieľa 56%, bielych 84%. V cieli bol pomer počtu čiernych a bielych potkanov 1 : 2. Aký bol pomer počtu čiernych a bielych potkanov na štarte?

Z9-II-4
Na úsečke PQ je jednou stranou položený štvorec MNOP (pozri obrázok). Priamka PQ sa postupne preklápa po stranách štvorca MNOP, pričom bod Q zanecháva na papieri stopu. Po prvom preklopení je táto stopa dlhá 5 cm, po piatich preklopeniach bod Q splynie s jedným z vrcholov štvorca. Určte dĺžku celej stopy bodu Q.

Z9-III-1
Michaela a Jana dnes obe majú narodeniny, dokopy majú 84 rokov. Pritom Michaela má dvakrát viac rokov, ako mala Jana, keď Michaela mala toľko rokov, koľko má Jana dnes. Koľko rokov má Michaela a koľko Jana?

Z9-III-2
Pred Janom sedeli tri zahalené princezné a Jano mal za úlohu zistiť, ktorá z nich je Zlatovláska.

Princezná v prvom kresle povedala:   „V treťom kresle Zlatovláska nesedí.“
Princezná v druhom kresle povedala:   „Ja Zlatovláska nie som.“
Princezná v treťom kresle povedala:   „Ja som Zlatovláska.“

Zázračná muška Janovi prezradila, koľko princezien klamalo. Až s touto radou dokázal Jano odhaliť pravú Zlatovlásku. Ktorá z princezien bola Zlatovláska?

Z9-III-3
Veliteľ zvolal ostatných obrancov hradu a rozhodol, ako sa rozdelia o svoju odmenu:

„Prvý si vezme jeden dukát a sedminu zvyšku, druhý si vezme dva dukáty a sedminu nového zvyšku a tak ďalej. Teda n-tý obranca si vezme n dukátov a k tomu ešte sedminu zo zvyšného množstva dukátov, pokiaľ nejaké budú.“

Takto sa podarilo rozdeliť všetky dukáty a pritom všetci obrancovia dostali rovnako. Koľko obrancov sa delilo o odmenu?

Z9-III-4
V rovnoramennom trojuholníku ABC je základňa AB dlhá 6 cm a uhol BCA má veľkosť 45◦. Vypočítajte polomer kružnice opísanej tomuto trojuholníku.

 

Uložiť

Uložiť