aktualizované 18.2.2017 15:35
| C | B | A |
| domáce kolo | domáce kolo | domáce kolo |
| školské kolo | školské kolo | školské kolo |
| krajské kolo | krajské kolo | krajské kolo |
| celoštátne kolo | ||
| Zadania úloh domáceho kola vo formáte PDF: |
||
C-I-1
Dokážte, že pre ľubovoľné reálne číslo a platí nerovnosť
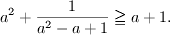
C-I-2
Nájdite najväčšie prirodzené číslo d, ktoré má tú vlastnosť, že pre ľubovoľné prirodzené číslo n je hodnota výrazu
deliteľná číslom d.
C-I-3
Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1 : 2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť
C-I-4
Nájdite všetky trojčleny P(x) = ax2 + bx + c s celočíselnými koeficientmi a, b, c, pre ktoré platí P(1) < P(2) < P(3) a zároveň
C-I-5
V danom trojuholníku ABC zvoľme vnútri strany AC body K, M a vnútri strany BC body L, N tak, že
Ďalej označme E priesečník uhlopriečok lichobežníka ABLK, F priesečník uhlopriečok lichobežníka KLNM a G priesečník uhlopriečok lichobežníka ABNM. Dokážte, že body E, F a G ležia na ťažnici trojuholníka ABC z vrcholu C a určte pomer |GF|:|EF|.
C-I-6
a) Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnoramenného trojuholníka. Marienka chce rozmiestniť cukríky tak, aby ich dostala čo najviac, nech už Peter trojicu vrcholov vyberie akokoľvek. Koľko ich tak Marienka zaručene získa?
b) Rovnakú úlohu vyriešte aj pre pravidelný deväťuholník, do ktorého vrcholov rozmiestni Marienka 1 až 9 cukríkov. (Medzi rovnoramenné trojuholníky zaraďujeme aj trojuholníky rovnostranné.)
|
|
 |
C-S-1
C-S-2
C-S-3
|
|
 |
C-II-1
C-II-2
C-II-3
C-II-4
|
|
 |
B-I-1
B-I-2
B-I-3
B-I-4
B-I-5
B-I-6
|
|
 |
B-S-1
B-S-2
B-S-3
|
|
 |
B-II-1
B-II-2
B-II-3
B-II-4
|
|
 |
A-I-1
Nájdite všetky prvočísla p, pre ktoré existuje prirodzené číslo n také, že pn + 1 je treťou mocninou niektorého prirodzeného čísla.
A-I-2
Máme n2 prázdnych škatúľ; každá z nich má štvorcové dno. Výška aj šírka každej škatule je prirodzené číslo z množiny {1,2,… ,n}. Každé dve škatule sa líšia aspoň v jednom z týchto dvoch rozmerov. Jednu škatuľu je dovolené vložiť do druhej, ak má oba rozmery menšie a aspoň jeden z rozmerov má aspoň o 2 menší. Takto môžeme vytvoriť postupnosť škatúľ vložených navzájom do seba (t. j. prvá škatuľa je vnútri druhej, druhá škatuľa je vnútri tretej atď.). Každú takúto sadu uložíme na inú poličku. Určte najmenší možný počet poličiek potrebný na uskladnenie všetkých n2 škatúľ.
A-I-3
Daný je ostrouhlý trojuholník ABC s výškami AK, BL, CM. Dokážte, že trojuholník ABC je rovnoramenný práve vtedy, keď platí rovnosť
A-I-4
A-I-5
Vnútri základne AB rovnoramenného trojuholníka ABC leží bod D. Zvoľme bod E tak, aby ADEC bol rovnobežník. Na polpriamke opačnej k ED leží bod F taký, že |EB| = |EF|. Dokážte, že dĺžka tetivy, ktorú vytína priamka BE na kružnici opísanej trojuholníku ABF, je dvojnásobkom dĺžky úsečky AC.
|
|
 |
A-S-1
Zistite, aké najmenšie kladné celé číslo možno vložiť medzi dvojčíslia 20 a 16 tak, aby výsledné číslo bolo násobkom čísla 2016.
A-S-2
Nájdite všetky kladné celé čísla n, pre ktoré sa dajú čísla 1, 2, …, n rozdeliť do troch disjunktných neprázdnych množín s navzájom rôznymi počtami prvkov tak, že v ľubovoľnej dvojici množín má tá s menším počtom prvkov väčší súčet svojich prvkov.
A-S-3
Body D a E sú (v tomto poradí) pätami výšok z vrcholov B a C ostrouhlého trojuholníka ABC. Predpokladajme, že platí |AE|•|AD| = |BE|•|CD|. Akú najmenšiu veľkosť môže mať uhol BAC?
|
|
 |
A-II-1
A-II-2
A-II-3
A-II-4
|
|
 |
