55. ročník matematickej olympiády 2005-2006
Súťažné úlohy kategórií Z4-Z9
Z4-I-1
Jurko rád kreslí autíčka. V pondelok namaľoval niekoľko autíčok, v utorok ich namaľoval trikrát toľko ako v pondelok, ale potom 12 pondelkových vygumoval. V stredu mal zlú náladu, nič nenamaľoval a ešte roztrhal polovicu utorkových, čiže 24. Koľko autíčok namaľoval v utorok? Koľko autíčok namaľoval v pondelok, v utorok a v stredu spolu?
(M. Dillingerová)
Z4-I-2
Z čísla 9 635 347 vyškrtni niekoľko číslic tak, aby vzniklo čo najväčšie číslo a súčet všetkých jeho číslic bol menší ako 20.
(M. Dillingerová)
Z4-I-3
Rozprávkový nafukovací štvorec, ktorý vie rozprávať, mal pred 5 minútami dĺžku strany 8 cm. Pri každom klamstve zväčší svoj obvod dvojnásobne. Pri každej vyslovenej pravde sa zmenší dĺžka každej jeho strany o 2 cm. Za posledných 5 minút 2-krát klamal a 2-krát hovoril pravdu.
a) Aký najväčší obvod môže mať teraz?
b) Aký najmenší obvod môže mať teraz?
(S. Bodláková)
Z4-I-4
Peter má na papier napísať z čísel od 1 do 200 všetky také, ktoré sa dajú deliť piatimi bezo zvyšku, ale nedajú sa deliť bezo zvyšku siedmimi. Pavol má vypísať z čísel od 1 do 200 všetky také, ktoré po delení siedmimi dávajú zvyšok 5. Koľko čísel má napísať Peter a koľko Pavol?
(M. Smitková)
Z4-I-5
Žabka Rosnička stála na rebríku, ktorý mal 5 priečok, na tretej priečke. Urobila šesť skokov a zostala stáť na piatej priečke. Vypíš všetky možnosti, ako mohla Rosnička skákať, ak vždy skočila len o jednu priečku hore alebo o jednu priečku dole.
(S. Bodláková)
Z4-I-6
Majka má v stavebnici len rovnako veľké kocky s hranou dĺžky 3 cm. Keď z nich postaví vežu, ktorá má na každom podlaží 4 kocky, bude mať veža výšku 54 cm. Aká vysoká by bola iná veža z takého istého počtu rovnakých kociek, ktorá by mala v každom podlaží deväť kociek?
(M. Dillingerová)
Z4-II-1
Z čísla 9 635 347 vyškrtni niekoľko číslic tak, aby vzniklo čo najmenšie číslo a aby súčet všetkých jeho číslic bol väčší ako 23.
(M. Dillingerová)
Z4-II-2
Rozprávkový nafukovací obdĺžnik, ktorý vie rozprávať, mal pred 5 minútami dĺžky strán 8 cm a 10 cm. Pri každom klamstve zväčší jednu dvojicu svojich rovnako dlhých strán dvojnásobne. Pri každej vyslovenej pravde sa zmenší dĺžka každej jeho strany o 3 cm. Za posledných 5 minút 1-krát klamal a 2-krát hovoril pravdu.
a) Aký najväčší obvod môže mať teraz?
b) Aký najmenší obvod môže mať teraz?
(S. Bodláková, M. Dillingerová)
Z4-II-3
Kubkovi sa páčia čísla, ktoré dávajú po delení piatimi zvyšok 1. Lukáškovi sa páčia čísla, ktoré nemajú žiadne dve číslice rovnaké. Napíš najmenšie trojciferné číslo, ktoré sa bude páčiť aj Kubkovi aj Lukáškovi.
(S. Bednářová)
Z5-I-1
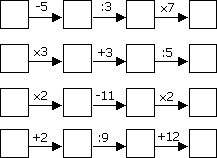
Doplň do prázdnych políčok prirodzené čísla od 1 do 20 (každé číslo môžeš použiť len raz) tak, aby platili matematické vzťahy.

(M. Smitková)
Z5-I-2
Blcha Skákalka skáče po vodorovnej číselnej osi. Vie robiť iba skoky dvoch dĺžok. Jedným preskočí o 14 doprava alebo doľava, druhým preskočí o 18 doprava alebo doľava. Práve stojí na čísle 2.
a) Nájdi spôsob, ako má skákať, aby sa štyrmi skokmi dostala na číslo 10.
b) Tvrdí, že včera bola na čísle 13. Hovorí pravdu alebo klame? Zdôvodni.
(M. Dillingerová)
Z5-I-3
Rozprávkový nafukovací štvorec, ktorý vie rozprávať, mal pred 5 minútami dĺžku strany 8 cm. Pri každom klamstve zväčší svoj obvod dvojnásobne. Pri každej vyslovenej pravde sa zmenší dĺžka každej jeho strany o 2 cm. Za posledných 5 minút 2-krát klamal a 2-krát hovoril pravdu.
a) Aký najväčší obvod môže mať teraz?
b) Aký najmenší obvod môže mať teraz?
(S. Bodláková)
Z5-I-4
Peťo si kúpil na jarmoku 4 autíčka, biele, zelené, červené a modré. Biele autíčko stálo dvakrát toľko ako červené, zelené trikrát toľko ako biele a za modré zaplatil toľko ako za červené a biele spolu. Pritom červené stálo o 70 Sk menej ako zelené. Koľko Sk stáli jednotlivé autíčka?
(Š. Ptáčková)
Z5-I-5
Mama stonožka má dve deti a manžela. Každý z nich má sto nôh a každý člen rodiny si berie každý deň čisté ponožky. V sobotu ráno o 6:00 začala mamička stonožka prať špinavé ponožky. Naraz sa jej ich do práčky zmestí 357 a jedna várka sa operie za dve a pol hodiny. Zisti, kedy skončí s praním, ak vieš, že ponožky perie raz za týždeň, uloženie ponožiek do práčky jej trvá 2 minúty a ich vybratie z práčky 3 minúty.
(S. Bednářová)
Z5-I-6
Mamička má v chladničke tehlu syra (viď obrázok). Postupne z nej odrezáva 1 cm hrubé plátky na vyprážanie. Najprv odrezala spredu plátok s rozmermi pre otecka, potom odrezala zboku pre Jurka, zozadu pre seba a nakoniec z druhého boku pre Aničku. Napíš, aké rozmery majú jednotlivé plátky. Urči rozmery zvyšku syra.

(M. Dillingerová)
Z5-II-1
Doplň do prázdnych políčok prirodzené čísla od 1 do 16 (každé číslo môžeš použiť len raz) tak, aby platili matematické vzťahy.
(M. Smitková)
Z5-II-2
Peter zlepil 17 hracích kociek do hada (ako na obrázku). Kocky zliepal vždy tak, že zlepil steny s rovnakým počtom bodiek. Potom si hada obzrel zo všetkých strán a správne spočítal všetky bodky na jeho povrchu. Koľko mu vyšlo? (Súčet bodiek na protiľahlých stenách hracej kocky je 7.)
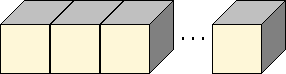
(S. Bodláková, M. Dillingerová)
Z5-II-3
Myslím si trojciferné prirodzené číslo menšie ako 200. Ak jeho trojnásobok zaokrúhlim na stovky, zväčší sa o 36. Ktoré číslo si myslím?
(M. Dillingerová)
Z6-I-1
Doplň do prázdnych políčok prirodzené čísla od 1 do 20 (každé číslo môžeš použiť len raz) tak, aby platili matematické vzťahy.

(M. Smitková)
Z6-I-2
Snehulienka so siedmimi trpaslíkmi zbierali lieskové oriešky. Snehulienka ich mala toľko ako všetci trpaslíci spolu. Keď sa vracali domov, stretli veveričku Finku. Snehulienka aj každý trpaslík jej dali rovnaký počet orieškov. Doma trpaslíci a Snehulienka vysypali oriešky na kôpky na stole, každý na inú kôpku a Vedko zapísal počty orieškov v kôpkach: 120, 316, 202, 185, 333, 297, 111 a 1672. Koľko orieškov dostala veverička Finka?
(L. Hozová)
Z6-I-3
Keď sme čísla 80 a 139 vydelili tým istým prirodzeným číslom, získali sme zvyšky 8 a 13. Ktorým číslom sme delili?
(M. Volfová)
Z6-I-4
Obvod trojuholníka je 16 cm. Aké môžu byť dĺžky jeho strán, keď sú to prirodzené čísla a súčet dĺžok dvoch strán je o 6 cm väčší ako dĺžka tretej strany?
(L. Hozová)
Z6-I-5
Maruška dostala päť rôzne ťažkých koláčov. Priemerná hmotnosť koláča bola 200 gramov. Maruška jeden koláč zjedla a priemerná hmotnosť zvyšných koláčov potom bola 160 gramov. Koľko gramov vážil koláč, ktorý Maruška zjedla?
(B. Šťastná)
Z6-I-6
Určte veľkosť plochy šedého štvoruholníka na obrázku, kde všetky rozmery sú udávané v centimetroch.

(P. Tlustý)
Z6-II-1
Pán Šikovný chcel v kúpeľni nafarbiť na 20 dlaždíc hviezdicové ornamenty (pozri jednu dlaždicu na obrázku). Na plechovke s farbou bolo napísané, že farba vystačí na 750 cm2. Koľko najmenej plechoviek musel pán Šikovný kúpiť, ak jeden štvorček siete má obsah 1 cm2.

(L. Hozová)
Z6-II-2
V jaskyni žije päť obrov. Ich priemerná výška je 15 504,63 cm. Obor Drobček meria 174,53 m, obor Lomikameň 173 530,5 mm, obor Zlobor 1 745,23 dm, obor Hrompác 0,017 34 km.
a) Zisti koľko meria piaty obor – Kolodej.
b) Zoraď obrov podľa veľkosti od najmenšieho po najväčšieho.
(S. Bednářová)
Z6-II-3
Snehulienka dala každému trpaslíkovi rovnako veľa guľôčiek. Trpaslíci potom hádzali kockou. Koľko im padlo bodiek, toľko guľôčiek museli vrátiť Snehulienke. Každému z prvých šiestich trpaslíkov padol iný počet bodiek, takže každý z nich vrátil Snehulienke iný počet guľôčiek. Koľko bodiek padlo poslednému trpaslíkovi, ak všetkým siedmim trpaslíkom po tomto hode ostalo spolu 46 guľôčiek? Koľko guľôčiek dala Snehulienka každému trpaslíkovi na začiatku?
(S. Bednářová)
Z7-I-1
Pat a Mat upravovali nový asfalt na ceste. Najprv išli s valcom 10 m dopredu, potom 7 m cúvli, opäť prešli 10 m dopredu a 7 m cúvli… Takto pokračovali, až kým po prvý raz nezišli z nového asfaltu.
a) Koľko metrov najazdil valec na novom 540 metrovom úseku cesty?
b) Koľkokrát prešli po devätnástom metri nového asfaltu?
(M. Dillingerová)
Z7-I-2
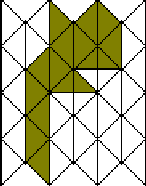
Zistite obsah a veľkosti všetkých vnútorných uhlov mnohouholníka znázorneného v kosoštvorcovej sieti na obrázku, ak viete, že priamky siete zvierajú uhol 80 stupňov a jeden malý kosoštvorček má obsah 1 cm2.
(Pozor, obrázok je nepresný, neoplatí sa merať.)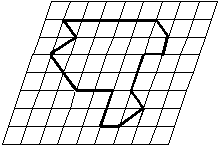
(S. Bednářová)
Z7-I-3
Na obrázku vidíte špeciálny druh rolády, tzv. KVADRILÁDU. Je vyrobená z bielej a hnedej marcipánovej hmoty, pričom obe hmoty majú rovnakú hrúbku 1 cm. Celá kvadriláda má dĺžku 15 cm. Predáva sa rozkrájaná na 10 rovnakých plátkov, pričom sa krája rovnobežne s prednou stenou. Zistite
a) rozmery jedného plátku,
b) koľko gramov hnedej hmoty a koľko gramov bielej hmoty treba na jej prípravu, ak viete, že jeden cm3 marcipánovej hmoty váži 2 gramy.
(Neoznačená šípka v obrázku má dĺžku 2 cm.)
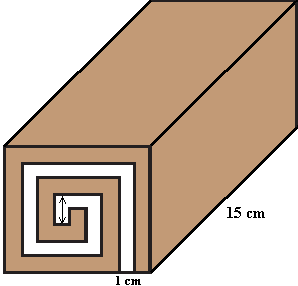
(S. Bednářová)
Z7-I-4
Nájdite všetky päťciferné čísla, ktoré sa škrtnutím prvej a poslednej cifry zmenšia 250-krát.
(L. Šimůnek)
Z7-I-5
Pavol dostal na domácu úlohu vyjadriť desatinným číslom zlomky  a
a 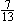 . Aby urobil pani učiteľke radosť, písal úlohu miesto do zošita na latky školského plota. Najprv vyjadroval
. Aby urobil pani učiteľke radosť, písal úlohu miesto do zošita na latky školského plota. Najprv vyjadroval  , teda na prvú latku navrch napísal 0, na druhú desatinnú čiarku, na tretiu 4 atď. Keď skončil, napísal pod tieto čísla vyjadrenie zlomku
, teda na prvú latku navrch napísal 0, na druhú desatinnú čiarku, na tretiu 4 atď. Keď skončil, napísal pod tieto čísla vyjadrenie zlomku 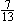 . Na prvú latku dole napísal 0, na druhú desatinnú čiarku, na tretiu 5 atď. Koľko bolo latiek na plote, ak viete, že číslicu 5 napísal presne 667 krát a že na 668 latkách bola dvojica rovnakých čísel.
. Na prvú latku dole napísal 0, na druhú desatinnú čiarku, na tretiu 5 atď. Koľko bolo latiek na plote, ak viete, že číslicu 5 napísal presne 667 krát a že na 668 latkách bola dvojica rovnakých čísel.
(M. Dillingerová, P. Tlustý)
Z7-I-6
V Kocúrkove majú dve zmenárne. V súčasnosti majú takéto kurzy:
| 1. zmenáreň |
2. zmenáreň |
| MENA |
NÁKUP |
PREDAJ |
MENA |
NÁKUP |
PREDAJ |
| 1 euro |
123 Kk |
132 Kk |
1 euro |
143 Kk |
154 Kk |
Slavo Špakulatý mal niekoľko euro. V 2. zmenárni ich zamenil za Kocúrkovské koruny (Kk) a tie potom zamenil v 1. zmenárni späť na euro. Takto zarobil 1 euro. Koľko euro mal na začiatku?
(S. Bednářová)
Z7-II-1
Sieť na obrázku je zložená zo zhodných rovnoramenných trojuholníkov. Každý z nich má obsah 2 cm2 a jeden z vnútorných uhlov trojuholníkov meria 100°. Zisti obsah a veľkosť vnútorných uhlov mnohouholníka znázorneného v tejto trojuholníkovej sieti. (Pozor, obrázok môže byť veľmi nepresný.)
Z7-II-2
Nájdi všetky štvorciferné čísla, ktoré sa škrtnutím prostredných dvoch cifier zmenšia 120-krát.
Z7-II-3
Kráľ Originál I. si sám navrhol a dal vybudovať bazén. Na obrázku vidíš, ako vyzerá jeho bazén pri pohľade zhora. Dno je pokryté štvorcovými dlaždicami so stranou dĺžky 2 m, betónové steny sú 3 m vysoké a 0,5 m hrubé. Zisti, koľko kg betónu spotrebovali na steny bazénu, ak 1 m3 betónu má hmotnosť 2000 kg.
Z8-I-1
Určte všetky dvojciferného čísla, pre ktoré súčin ciferného súčtu a ciferného súčinu je 126.
(M. Raabová)
Z8-I-2
Pani Zručná sa uchádzala o miesto vo výrobe vianočných perníkov. Pri pohovore s vedúcim chcela povedať, koľko perníkov ozdobí za koľko minút. Bola nervózna, a preto omylom prehodila počet minút s počtom perníkov. Vedúci podľa jej údajov vypočítal, koľko perníkov by mala pani Zručná stihnúť ozdobiť za päťhodinovú pracovnú dobu, a presne tento počet jej dal za úlohu ozdobiť. Pani Zručnej trvala práca o 2 hodiny a 12 minút dlhšie. Koľko perníkov ozdobila?
(L. Šimůnek)
Z8-I-3
Na obrázku vidíte špeciálny druh rolády, tzv. KVADRILÁDU. Je vyrobená z bielej a hnedej marcipánovej hmoty, pričom obe hmoty majú rovnakú hrúbku 1 cm. Celá kvadriláda má dĺžku 15 cm. Predáva sa rozkrájaná na 10 rovnakých plátkov, pričom sa krája rovnobežne s prednou stenou. Zistite
a) rozmery jedného plátku,
b) koľko gramov hnedej hmoty a koľko gramov bielej hmoty treba na jej prípravu, ak viete, že jeden cm3 marcipánovej hmoty váži 2 gramy.
(Neoznačená šípka v obrázku má dĺžku 2 cm.)
(S. Bednářová)
Z8-I-4
Roman písal na papier za sebou celé čísla tak, že nasledujúce získal z predchádzajúceho striedavo násobením dvoma a odčítaním troch. Napr. postupnosť čísel 1; 2; -1; -2; -5; -10 vyhovuje jeho pravidlu, ale postupnosť 10; 7; 4; 8; 16; 32 jeho pravidlo nesplňuje. Po chvíli sčítal posledných 5 čísel, ktoré napísal a vyšlo mu 114. Ktorých 5 čísel sčitoval?
(M. Raabová)
Z8-I-5
Určte polomer väčšej kružnice na obrázku, ak každá malá kružnica má polomer 1 cm.
(P. Tlustý)
Z8-I-6
Jakub má tento školský rok priemer všetkých svojich známok 1,85. Za celý školský rok dostal iba štyri pätorky a práve tretina jeho známok boli jednotky. Najmenej koľko známok musel tento školský rok dostať?
(L. Šimůnek)
Z8-II-1
Každé písmeno tabuľky nahrádza určité prirodzené číslo (rovnaké písmená nahrádzajú rovnaké čísla). Súčet čísel v treťom riadku je 50. Súčet čísel vo štvrtom riadku je 45. Súčet čísel v prvom stĺpci je 85. Určte aspoň jednu vyhovujúcu štvoricu čísel, ktorou možno nahradiť písmená A, B, C, D. Určte súčet všetkých čísel v tabuľke.
| D |
A |
C |
B |
| C |
B |
D |
A |
| B |
C |
B |
C |
| D |
A |
A |
A |
Z8-II-2
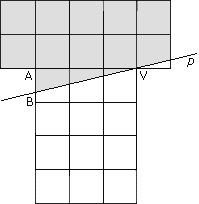
Máme obrazec tvaru T zložený z 22 štvorčekov so stranou dĺžky 1 cm. Bodom V sme viedli priamku p, ktorá rozdelila obrazec na dve časti rovnakého obsahu. V akom pomere rozdeľuje priamka p úsečku AB?
Z8-II-3
Majka vytvorila postupnosť čísel, v ktorej je každé číslo (s výnimkou prvého) súčtom druhých mocnín číslic predchádzajúceho čísla. Vypíš prvých 10 členov tejto postupnosti, ak jej prvým členom je číslo 29. Ktoré číslo je v postupnosti na 2006. mieste?
Z9-I-1
Určte počet trojciferných prirodzených čísel, ktoré majú práve dve rovnaké cifry.
(P. Tlustý)
Z9-I-2
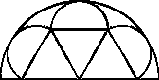
Na obrázku sú tri rovnostranné trojuholníky, jedna veľká polkružnica s polomerom 1 dm a tri malé polkružnice. Určte dĺžku úsečky AB.
(P. Tlustý)
Z9-I-3
V súradnicovej sústave sme znázornili body A[3; 2], B[-1; 1], C[-2; 4] a ich obrazy A´, B´, C´ v stredovej súmernosti so stredom v začiatku súradnicovej sústavy. Vypočítajte obsah šesťuholníka ABCA´B´C´.
(S. Bednářová)
Z9-I-4
Starý podnikateľ zomrel a zanechal po sebe dva účty, jeden dlh a testament. V testamente sa písalo, že peniaze z prvého účtu si majú rozdeliť 1. a 2. syn v pomere 1:2, peniaze z druhého účtu 1. a 3. syn v pomere 1:3 a dlh majú zaplatiť 2. a 3. syn v pomere 2:3. Zistite, koľko Sk bolo na jednotlivých účtoch a aký dlh museli synovia splatiť, ak viete, že v konečnom dôsledku každý z nich získal 123 456 Sk.
(S. Bednářová)
Z9-I-5
br />
Dva rovnostranné papierové trojuholníky, z ktorých menší má obsah 60 cm2, sme položili cez seba tak, že ich prienikom bol pravouhlý trojuholník s obsahom 30 cm2. Aký najmenší obsah mohol mať väčší z rovnostranných trojuholníkov?
(S. Bednářová)
Z9-I-6
Zadanie písomnej práce obsahovalo 26 otázok, ktoré boli rozdelené podľa obtiažnosti do troch skupín. V prvej skupine bola správna odpoveď hodnotená tromi bodmi, v druhej piatimi bodmi a v tretej ôsmimi bodmi. Maximálny možný počet získaných bodov bol 111. Koľko otázok mohlo byť v každej skupine?
(L. Šimůnek)
Z9-II-1
Peter a Jano išli plávať. Vzdialenosti, ktoré odplávali, boli v pomere 4:5. (Jano odplával viac.) Ďalší deň šli opäť plávať, teraz preplával Peter o 200 metrov menej a Jano o 100 metrov viac ako predchádzajúci deň. Pomer vzdialeností za druhý deň bol 5:8. Koľko metrov preplával prvý deň Peter a koľko Jano?
(B. Šťastná)
Z9-II-2
Určte obsah šedej plochy na obrázku, ak každý z troch bielych kruhov má polomer 1 cm a úsečky, ktoré plochu ohraničujú, sú ich dotyčnicami.
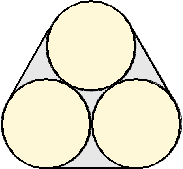
(P. Tlustý)
Z9-II-3
Marek má kalkulačku, ktorá prevedie počtové úkony v takom poradí, v akom ich Marek zadáva. Na papier si napísal jedno číslo. Zadal ho do kalkulačky a potom postupne stláčal tlačidlá

Výsledok odpísal z displeja na papier. Potom s napísaným číslom urobil to isté ako s predchádzajúcim číslom, teda zadal ho do kalkulačky a stláčal plus, štyri, delené, štyri, mínus, štyri, krát, štyri. Výsledok si zapísal na papier. Celý postup s týmto novo získaným číslom zopakoval a výsledok opäť zapísal na papier. Potom zistil, že súčet štyroch čísel zapísaných na papieri je 80. Ktoré čísla a v akom poradí zapisoval Marek na papier?
(M. Raabová)
Z9-II-4
V rovnostrannom trojuholníku vyznačte každý bod, ktorého vzdialenosť od najbližšieho vrcholu je menšia ako vzdialenosť od ťažiska. Koľko percent plochy rovnostranného trojuholníka tvoria všetky vyznačené body?
(L. Šimůnek)
Z9-III-1
Doplňte do štvorčekov prirodzené čísla tak, aby:
• súčet všetkých doplnených čísel bol 44,
• súčet čísel v každom štvorci zloženom zo štyroch štvorčekov bol rovnaký,
• najmenšie doplnené číslo bolo nepárne,
• uprostred štvorca bolo jednociferné číslo.
(S. Bednářová)
Z9-III-2
Určte obsah šedého mesiačika z obrázku, ak viete, že priemer veľkého polkruhu má dĺžku |CD| = 2 cm, priemer menšieho polkruhu má dĺžku |AB| = 1 cm a platí AB || CD.
(P. Tlustý)
Z9-III-3
Jakub mal v pivnici tri krabice tvaru kvádra so štvorcovou podstavou. Prvá bola dvojnásobne vyššia ako druhá. Druhá bola jeden a pol násobne širšia ako prvá. Tretia bola trojnásobne vyššia ako prvá a dvojnásobne užšia ako prvá. V akom pomere sú objemy nádob?
(Š. Ptáčková)
Z9-III-4
Pri prijímacích skúškach na univerzitu sa každému záujemcovi o štúdium prideľuje krycí kód zložený z piatich číslic. Skúšky organizoval dôkladný, ale poverčivý docent, ktorý sa pred prideľovaním kódov rozhodol vyradiť zo všetkých možných kódov (t.j. 00000 až 99999) tie, ktoré v sebe obsahovali číslo 13, teda číslicu 3 bezprostredne nasledujúcu po číslici 1. Koľko kódov musel docent vyradiť?
(L. Šimůnek)