56. ročník matematickej olympiády 2006-07 (kategórie Z4-Z9)
| Z4 | Z5 | Z6 | Z7 | Z8 | Z9 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | |||||
Z4-I-1
Na obrázku sú v štvorčekovej sieti znázornené dva ZUBOUHOLNÍKY (svetlosivý a tmavosivý), ktoré sa zahryzli do seba. (ZUBOUHOLNÍK je špeciálny druh mnohouholníka.) Zistite, ktorý z nich má väčší obsah a ktorý obvod.
Z4-I-2
Miss STRANGELANDIA dostala tak veľa rôznych ponúk od rôznych modelingových agentúr, že si z nich nevedela vybrať. Napokon sa rozhodla, že prijme ponuku tej z nich, ktorá ako prvá uhádne číslo jej topánok. Prezradila im, že je to dvojciferné číslo s ciferným súčtom 12 a že, keby sa v tomto čísle zmenilo poradie číslic, vzniklo by číslo o 54 väčšie. Aké číslo topánok nosí Miss STRANGELANDIA?
Z4-I-3
Jurko včera na magnetickej tabuli vytvoril vzorový príklad. Dnes, keď prišiel do školy, zistil, že pani upratovačka ho „upratala“ a všetky použité číslice a znaky zoradila na dolnom okraji tabule takto:
3 4 5 6 8 9 + =
Aký príklad vytvoril včera Jurko? Nájdi všetky možnosti.
Z4-I-4
Rodičia prvej slovenskej superstar K.K. sa starajú o jaskyňu „Zlá diera„. V jaskyni je tma, návštevníci si svietia karbidovými lampášikmi. Pre seba a pre pani učiteľku má pán Košč väčšiu lampičku. Lampášikov však mali len 9, preto sprievodca pán Košč zoradil našu skupinu ako husi tak, že tesne pred tým, kto nemal lampášik, išiel niekto s lampášikom alebo lampičkou. Prvý v zástupe bol on, posledná pani učiteľka s lampičkou. Lampášik niesli 4 chlapci, 4 dievčatá lampášik nedostali. Koľko dievčat bolo v našej skupine? Koľko tam bolo chlapcov?
Poznámka: Nik neniesol dva lampášiky, a žiadni dvaja s lampášikmi nešli tesne za sebou.
Z4-I-5
Sedem Snehulienkiných trpaslíkov bolo na hríboch. Prišli s košíčkami, v ktorých mali 34, 19, 50, 44, 31, 28 a 37 hríbov. Snehulienka im povedala, aby niektoré košíčky uložili do špajze, niektoré dali ku sporáku a ostatné položili na stôl tak, že všade malo byť rovnako veľa hríbov. Trpaslíci sa rozhodli, že hríby z košíčkov nebudú vyberať. Podarí sa im uložiť košíčky tak, ako to chcela Snehulienka? Nájdi aspoň jeden spôsob.
Z4-I-6
Z čísla 1583719 vyškrtni tri číslice tak, aby vzniklo čo najväčšie číslo, ktorého každá číslica je nepárna.
Z4-II-1
Na obrázku sú v štvorčekovej sieti znázornené dva ZUBOUHOLNÍKY (svetlosivý a tmavosivý), ktoré sa zahryzli do seba. (ZUBOUHOLNÍK je špeciálny druh mnohouholníka.) Zistite, ktorý z nich má väčší obsah a ktorý má väčší obvod.
Z4-II-2
V stánku s kvetmi majú ruže, tulipány a klinčeky (a žiadne iné kvety). Ruží je o 12 viac ako tulipánov a tulipánov je o 6 menej ako klinčekov. Spolu je v stánku 60 kvetov. Koľko z tohto počtu je ruží? Koľko je tulipánov a koľko klinčekov?
Z4-II-3
Z čísel 1523 a 6346 vyškrtni spolu dve číslice tak, aby súčet vzniknutých čísel bolo čo najväčšie číslo, ktorého každá číslica je nepárna.
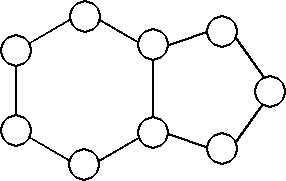
Z5-I-1
Na obrázku číslo vidíš päťuholník a šesťuholník so spoločnou stranou. Doplň do krúžkov na tomto obrázku čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 tak, aby súčet čísel v šesťuholníku aj súčet čísel v päťuholníku bol 24. Každé číslo smieš použiť len raz. Stačí, keď nájdeš jedno riešenie.
Z5-I-2
Cyklistického preteku Krížom – krážom sa zúčastnili šesťčlenné družstvá z celej Európy. Prvých desať etáp ešte zvládli všetci, ale v jedenástej etape po hromadnom páde odstúpilo 17 cyklistov. V každej ďalšej etape ich potom odstúpilo o troch menej ako v predošlej. Do cieľa poslednej, 15. etapy, došlo 53 cyklistov. Koľko družstiev sa zúčastnilo preteku?
Z5-I-3
Tomáškova cvičená blcha Skákalka stála na ciferníku hodín na bodke pri čísle 12. Hrala sa s ním takúto hru: Tomáško hodil kockou a blcha skočila o toľko bodiek ďalej, koľko mu padlo na kocke. Ale po prvom hode skákala v smere pohybu hodinových ručičiek, po druhom proti smeru a po treťom opäť v smere pohybu hodinových ručičiek. Vieme, že Tomáško hodil dvojku, päťku a šestku, ale nevieme, v akom poradí mu padli.
a) Na bodke pri ktorom čísle mohla skončiť Skákalka po treťom skoku?
b) Na ktoré číslo sa blcha počas hry vôbec nemohla dostať?
Z5-I-4
Pomocou číslic 0 až 9 a dvoch desatinných čiarok utvor dve desatinné čísla tak, aby ich súčet bol čo najmenší. Nájdi všetky možnosti! (Každú číslicu treba použiť práve raz!)
Z5-I-5
Sedem Snehulienkiných trpaslíkov bolo na hríboch. Prišli s košíčkami, v ktorých mali 34, 19, 50, 44, 31, 28 a 37 hríbov. Snehulienka im povedala, aby niektoré košíčky uložili do špajze, niektoré dali ku sporáku a ostatné položili na stôl tak, že všade malo byť rovnako veľa hríbov. Trpaslíci sa rozhodli, že hríby z košíčkov nebudú vyberať. Podarí sa im uložiť košíčky tak, ako to chcela Snehulienka? Nájdi aspoň jeden spôsob.
Z5-I-6
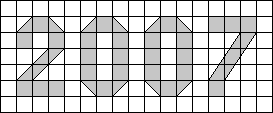
Na obrázku je v štvorčekovej sieti znázornené číslo 2007. Zisti obsah sivej časti obrázka, ak vieš, že strana každého malého štvorčeka meria 4 cm.
Z5-II-1
Dievčatá zbierali uzávery PET- fľaší. Šárka ich nazbierala 20, Svetlana 29, Marta 31, Maruška 49 a Monika 51. Každé z dievčat nasypalo všetky svoje nazbierané uzávery buď do modrej, alebo do červenej škatule. Paľko pri počítaní uzáverov zistil, že v modrej škatuli je dvakrát viac uzáverov ako v červenej. Ktoré dievčatá nasypali svoje uzávery do modrej a ktoré do červenej škatule?
Z5-II-2
Na obrázku sú znázornené 3 navzájom sa prekrývajúce štvorce. Zisti ich obsahy, ak vieš, že:
- strana najväčšieho štvorca je o 1 mm dlhšia, ako strana prostredného a o 2 mm dlhšia ako strana najmenšieho z nich,
- spoločná časť najväčšieho a prostredného štvorca je štvorec s obsahom 100 mm2,
- spoločná časť prostredného a najmenšieho štvorca je štvorec s obsahom 64 mm2.
(Pozor, obrázok môže byť veľmi nepresný, neoplatí sa ti merať.)
Z5-II-3
Na záhradke vyrástlo štyrikrát viac kalerábov ako brokolíc a trikrát viac reďkvičiek ako kalerábov. Celková hmotnosť brokolíc bola 5 kg. Koľko kusov zeleniny vyrástlo na záhradke, ak každá brokolica vážila 250 g? (Iná zelenina tam nerástla.)
Z6-I-1
Lukáš natieral latkový plot. Každých 10 minút natrel 8 latiek. Jeho mladší brat Kubko mu chvíľku pomáhal. Za 7 minút natrel vždy 4 latky, takže Lukáš skončil o štvrť hodiny skôr, ako predpokladal. Ako dlho mu Kubko pomáhal?
Z6-I-2
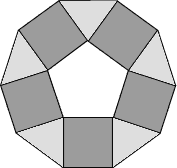
Zo zhodných rovnoramenných trojuholníkov a štvorcov sme zložili (bez prekrývania) útvar znázornený na obrázku. Zisti veľkosti vnútorných uhlov týchto rovnoramenných trojuholníkov.
Z6-I-3
Hviezda na obrázku v štvorcovej sieti je rozdelená dvomi úsečkami na tri časti. Zisti obsahy jednotlivých častí.
Z6-I-4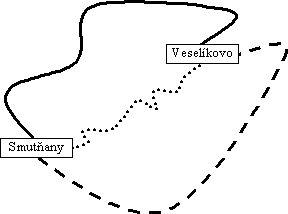
Zo Smutňan do Veselíkova vedú tri cesty. (pozri obrázok) Tá, ktorá je na mape vyznačená ako plná, meria 40 km, najvyššia povolená rýchlosť je na nej 80 km/h a vyberá sa na nej mýto 50 korún. „Bodkovaná“ cesta je dlhá 35 km, najvyššia povolená rýchlosť je na nej 60 km/h a mýtne je 150 korún. Na „čiarkovanej“ ceste, ktorá je dlhá 45 km sa vyberá mýto 100 korún a najvyššia povolená rýchlosť je 100 km/h. Ujo Ponáhľavý a teta Šporovlivá sa chcú dostať zo Smutňan do Veselíkova, ujo čo najskôr a teta čo najlacnejšie. Obaja si zavolali taxík. Šoféri taxíkov celú cestu idú maximálnou povolenou rýchlosťou a účtujú si 15 korún za jeden km cesty a zaplatené mýtne.
a) Ktorou cestou sa má vybrať taxikár uja Ponáhľavého?
b) Ktorou cestou sa má vybrať taxikár tety Šporovlivej?
c) O koľko minút menej bude trvať ujova cesta v porovnaní s tetinou?
d) O koľko korún viac zaplatí ujo ako teta?
Z6-I-5
Viacciferné číslo sa nazýva optimistické, ak jeho číslice zľava doprava rastú. Ak číslice čísla zľava doprava klesajú, hovoríme, že je to číslo pesimistické. Súčet sedemciferného pesimistického a sedemciferného optimistického čísla zloženého z tých istých číslic je 11001000. Ktoré číslice sme použili na zápis týchto dvoch čísel?
Z6-I-6
Naša trieda plánovala turistický výlet. Niektorí žiaci sa dohadovali o dĺžke jeho trasy a tvrdili, že je to 28, 16, 32, 37 a 15 km. Mýlili sa však o 5, 7, 8, 9 a 14 km. Aký dlhý bol výlet v skutočnosti?
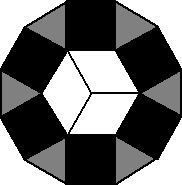
Z6-II-1
Zo zhodných sivých trojuholníkov a šiestich zhodných štvorcov sme zložili (bez prekrývania) útvar znázornený na obrázku. Do jeho stredu sa bez prekrývania zmestili tri zhodné štvoruholníky, každý s obsahom 4 cm2.
a) Zistite veľkosti vnútorných uhlov sivého trojuholníka.
b) Zistite obsah celej sivej plochy.
Z6-II-2
Cyril má o štvrtinu guliek viac ako Boris a ten o štvrtinu guliek viac ako Adam. Spolu majú 122 guliek. Koľko má každý z nich?
Z6-II-3
Viacciferné číslo sa nazýva optimistické, ak jeho číslice zľava doprava rastú. Ak číslice čísla zľava doprava klesajú, hovoríme, že je to číslo pesimistické. Súčet pesimistického a optimistického čísla zloženého z tých istých číslic je 109900, ich rozdiel je 84942. Ktoré sú to čísla?
Z7-I-1
Janka narysovala 6-uholník, ktorého dĺžky strán vyjadrené v cm sú celé čísla. Potom si uvedomila, že každé dve jeho susedné strany sú na seba kolmé. Zisti, ako mohol vyzerať Jankin 6-uholník, ak jeho obvod má byť 16 cm a jeho obsah má byť 12 cm2. Narysuj obe možnosti.
Z7-I-2
Rozdeľ obdĺžnik na obrázku, ktorý sa skladá z rovnakých štvorcov na čo najmenší počet zhodných častí tak, aby každá z nich obsahovala len také čísla, ktoré dávajú po delení tromi navzájom rôzne zvyšky. Pozor, rezať sa smie len po čiarach siete!
Z7-I-3
Urči počet zlomkov, ktorých hodnota je násobkom troch a čitateľ aj menovateľ sú trojciferné prirodzené čísla.
Z7-I-4
Rozprávkový deduško niesol vrece zrna do mlyna. Po ceste mu zrno začalo z vreca vypadávať. Tri vtáčiky si všimli, že za deduškom ostáva cestička označená jednotlivými zrnkami. Prvý išiel zobať zrnká zelený vtáčik a zozobal každé štvrté zrnko ležiace na zemi. Potom priletel zobať červený vtáčik a zozobal každé piate na zemi ležiace zrnko. Nakoniec zlietol na cestičku modrý vtáčik a zozobal každé tretie na zemi ležiace zrnko. Koľko zrniek stratil deduško z vreca, ak vtáčiky zozobali spolu 79 zrniek?
Z7-I-5
Troj- a viacciferné číslo s navzájom rôznymi ciframi, pre ktorého žiadne tri za sebou idúce číslice a, b, c neplatí a < b < c ani a > b > c, sa nazýva vlnité. Napíš
a) najväčšie vlnité číslo, ktoré nie je deliteľné 3,
b) najväčšie vlnité číslo deliteľné 150.
Z7-I-6
Osemboký kolmý hranol načrtnutý na obrázku vznikol zlepením troch kvádrov. Zisti objem a povrch tohto hranola, ak poznáš dĺžky vyznačených hrán a vieš, že z ôsmich jeho bočných stien sú vždy dve a dve zhodné.
Z7-II-1
Baba Jaga pripravila vzácny elixír. Na trhu ponúkala 6 fľaštičiek – o objeme 11 ml, 12 ml, 17 ml, 19 ml, 21 ml a 26 ml. Elixír bol však iba v piatich z nich. Jedna fľaštička obsahovala zafarbenú vodu. Prvý kupec si odniesol 2 fľaštičky s elixírom. Druhý získal tiež iba elixír a bolo ho dvakrát viac, než koľko si odniesol prvý kupec. Viac kupcov neprišlo a tak si baba Jaga musela svoju fľaštičku s vodou odniesť domov. Ktorá to bola? Koľko ml elixíru kúpil prvý, koľko druhý kupec?
Z7-II-2
Kríž na obrázku je rozdelený dvomi úsečkami na štyri diely. Určte obsah každého z nich.
Z7-II-3
Hanka sa hrá s tromi prázdnymi nádobami. Najprv naplnila vodou až po okraj najmenšiu a stredne veľkú nádobu. Túto vodu preliala z oboch nádob do najväčšej. Tým ju naplnila na 50%. Potom znovu naplnila vodou stredne veľkú nádobu až po okraj. Touto vodou najprv naplnila najmenšiu nádobu a celý zvyšok preliala do najväčšej, ktorú tým doplnila do 2/3 jej objemu. Aké sú objemy najmenšej a najväčšej nádoby, ak stredne veľká nádoba má objem 6 dl?
Z8-I-1
Z číslic 1 až 9 sme utvorili tri zmiešané čísla 
. Potom sme tieto tri čísla správne sčítali. Aký najmenší súčet sme mohli dostať?
(Každú číslicu sme použili práve raz!)
Z8-I-2
Pán kráľ si dal naliať plnú čašu vína. Pätinu vína z nej odpil. Potom si nechal čašu doplniť vodou a odpil štvrtinu objemu. Opäť mu ju doliali vodou a kráľ odpil tretinu. Nakoniec čašu ešte raz doliali vodou doplna. Koľko percent objemu čaše tvorí pôvodné víno?
Z8-I-3
Je daný pravidelný deväťuholník ABCDEFGHI. Vypočítajte veľkosť uhla, ktorý zvierajú priamky DG a BE.
Z8-I-4
Žiaci postavili z množstva rovnakých kociek pyramídu, ktorej časť vidíte na obrázku. Pyramída, svojho druhu najväčšia na svete, stála od tej doby na školskom dvore a pršalo na ňu. Po čase sa museli všetky kocky, na ktoré pršalo, teda tie na povrchu, vymeniť. Vymenilo sa celkom 2 025 kociek. Koľko mala pyramída vodorovných vrstiev?
Z8-I-5
Na lúke sa pásli ovce. Tých s rohami bolo dvakrát menej ako tých bez rohov. Tých s tmavým kožúškom bolo toľko ako tých so svetlým kožúškom. (Iné ovce, jednorohé, fľakaté a pod., sa na lúke nepásli.) Iba tri tmavé ovečky nemali rohy a svetlé vôbec nemali rohy. Koľko sa páslo ovečiek na lúke?
Z8-I-6
Výška rovnoramenného trojuholníka ABC delí tento trojuholník na dve časti, ktorých obsahy sú v pomere 1:3. Určte obsah a obvod trojuholníka ABC, ak viete, že |AC| = |BC| a |AB| = 
cm.
Z8-II-1
Doplňte na prázdne tehličky sčítacej pyramídy znázornenej na obrázku chýbajúce prirodzené čísla tak, aby práve dve z týchto doplnených čísel boli rovnaké. Nájdite všetky riešenia!
V sčítacej pyramíde sa na každej tehličke (okrem tých z najspodnejšieho riadku) nachádza súčet toho, čo je napísané na dvoch s ňou susediacich tehličkách z nižšieho riadku.
Z8-II-2
a) Zistite súčet všetkých dvojciferných čísel, ktorých druhá mocnina končí číslicou 9.
b) Nájdite všetky dvojciferné čísla, ktorých druhá mocnina končí dvojčíslím 44.
Z8-II-3
Do kružnice k so stredom O je vpísaný lichobežník ABCD (AB||CD), pričom priamka AC je osou uhla DAB. Ukážte, že potom |AD|=|CD| a navyše, priamka CO je osou uhla BCD.
Z9-I-1
Zistite, koľko je takých šesťciferných čísel, ktoré majú ciferný súčin 750?
Z9-I-2
V sčítacej pyramíde sa na každej tehličke (okrem tých z najspodnejšieho riadku) nachádza súčet toho, čo je napísané na dvoch s ňou susediacich tehličkách z nižšieho riadku. Doplňte na prázdne tehličky sčítacej pyramídy znázornenej na obrázku chýbajúce výrazy.
Z9-I-3
Do kružnice s polomerom 2 cm je vpísaný pravidelný šesťuholník ABCDEF. Priesečník priamok FE a CD označme M. Vypočítajte dĺžku úsečky AM.
Z9-I-4
Matematickej súťaže sa zúčastnilo 142 žiakov. Po skončení súťaže autor zistil, že priemerný počet bodov udelených za tretiu úlohu pripadajúci na jedného súťažiaceho je 2,7 (zaokrúhlené na desatiny). Nie každý súťažiaci však tretiu úlohu odovzdal, takže priemerný počet bodov udelených za tretiu úlohu pripadajúci na jedno odovzdané riešenie bol 3,9 (zaokrúhlené na desatiny). Koľko súťažiacich mohlo odovzdať tretiu úlohu?
Poznámka: Udeľovali sa len celé body, neodovzdaná úloha bola hodnotená 0 bodmi.
Z9-I-5
Trojuholník REZ s obsahom 300 cm2, stranou RE dĺžky 25 cm a stranou ZE dĺžky 30 cm sme dvomi priamymi rezmi rozdelili na 3 časti a z týchto častí zložili (bez prekrývania) obdĺžnik. Aké rozmery mohol mať tento obdĺžnik? Nájdite všetky možnosti.
Z9-I-6
Ukážte, že číslo
(1 . 3 . 5 . … . 2003 . 2005) + (2 . 4 . 6 . … . 2002 . 2004)
je deliteľné číslom 20074.
Z9-II-1
V súčinovej pyramíde sa na každej tehličke (okrem tých z najspodnejšieho riadku) nachádza súčin toho, čo je napísané na dvoch s ňou susediacich tehličkách z nižšieho riadku. Doplňte na prázdne tehličky súčinovej pyramídy znázornenej na obrázku chýbajúce výrazy. Výrazy píšte v čo najjednoduchšom tvare a uveďte, v akom poradí ste ich doplňovali.
Z9-II-2
Na obrázku vidíte bazén, s dlhým schodom pri jednej jeho stene. Prázdny bazén sme začali napúšťať prívodom s konštantným prietokom a sledovali sme výšku hladiny. Za 8 min hladina vystúpila do výšky 20 cm a dovtedy ešte nebola na úrovni schodu. Po 23 min napúšťania sa hladina nachádzala vo výške 55 cm od dna a schod už bol nejakú dobu pod hladinou. Po 35,5 min napúšťania bol bazén naplnený do výšky 80 cm. Aká je výška h schodu?
Z9-II-3
Nováková, Vašková a Sudková vyhrali štafetu a okrem diplomov dostali aj bonboniéru, ktorú hneď po závode zjedli. Keby zjedla Petra o 3 bonbóny viac, zjedla by ich práve toľko čo Miška s Janou dokopy. A keby si Jana pochutnala ešte na siedmich bonbónoch, tiež by ich mala toľko ako druhé dve spolu. Ešte vieme, že počet bonbónov, ktoré zjedla Vašková, je deliteľný tromi, a že Sudková si pochutila na siedmich bonbónoch. Ako sa volali dievčatá? Koľko bonbónov zjedla každá z nich?
Z9-II-4
Daný je obdĺžnik KLMN, kde |KL| = 6 cm a |ML| = 4 cm. Vypočítajte obvody všetkých rovnoramenných trojuholníkov KLX, ktorých vrchol X leží na strane MN.
Z9-III-1
Pavol si zvolil dve prirodzené čísla a vypočítal rozdiel ich druhých mocnín. Vyšlo mu 2007.
Ktoré dvojice čísel si mohol Pavel zvoliť?
Z9-III-2
V laboratóriu na polici stojí uzavretá sklenená nádoba tvaru kvádra. Nachádza sa v nej 2,4 litra destilovanej vody, ale objem nádoby je väčší. Voda v nádobe siaha do výšky 16 cm. Keď kvádrovú nádobu preklopíme na inú jej stenu, bude hladina vo výške 10 cm. Keby sme ju postavili na ešte inú stenu, voda by siahala iba do výšky 9,6 cm. Určte rozmery nádoby.
Z9-III-3
Prečítajte si výsledky ankety, pri ktorej bolo oslovených 1240 ľudí:
„V existenciu Yetiho verí 46 % opýtaných (zaokrúhlené na celé číslo), 31 % v jeho existenciu neverí (zaokrúhlené na celé číslo). Ostatní účastníci ankety odmietli na túto otázku akokoľvek reagovať.“
a) Koľko najmenej ľudí mohlo v ankete odpovedať, že veria v existenciu Yetiho?
b) Koľko najviac ľudí mohlo odmietnuť na anketu odpovedať?
Uveďte konkrétne počty, nie percentá.
Z9-III-4
Na obrázku sú znázornené 3 zhodné, navzájom sa prekrývajúce rovnostranné trojuholníky T1, T2, T3. Určte obsah každého z nich, ak viete, že súčasne platí:
- Prienikom trojuholníka T1 a trojuholníka T2 je rovnostranný trojuholník s obsahom
cm2. - Prienikom trojuholníka T2 a trojuholníka T3 je rovnostranný trojuholník s obsahom
cm2. - Prienikom trojuholníka T1 a trojuholníka T3 je rovnostranný trojuholník s obsahom
cm2.