57. ročník matematickej olympiády 2007-2008

Z4	Z5	Z6	Z7	Z8	Z9
1. kolo	1. kolo	1. kolo	1. kolo	1. kolo	1. kolo
2. kolo	2. kolo	2. kolo	2. kolo	2. kolo	2. kolo
					3. kolo

Z4-I-1
Z päťciferných čísel 53 827 a 19 763 vyškrtni spolu dve číslice tak, aby súčet vzniknutých čísel bol čo najväčší.

Z4-I-2
Na pomarančovú limonádu potrebujeme šťavu z ôsmich pomarančov, dvoch citrónov, 2 čajové lyžičky cukru a 6 decilitrov vody. Do džbánu sme si naliali 9 decilitrov vody. Koľko musíme odšťaviť pomarančov, citrónov, koľko pridať lyžičiek cukru, aby sme dostali rovnako kvalitnú limonádu?

Z4-I-3
Na drevenom plote je 70 latiek. Paľko s Aničkou ich mali všetky ponatierať farbou. Začali aj skončili obaja naraz. Kým Anička natrela dve latky, prešli 4 minúty a za 8 minút stihol Paľko ponatierať 3 latky. Ako dlho im trvalo natretie všetkých latiek?

Z4-I-4
Na obrázku s časťou štvorčekovej siete sú vyznačené tri body. Každé dva z tých troch vyznačených bodov tvoria vždy dva zo štyroch vrcholov nejakého štvorca. Štvorec KAMI je najmenší z nich, ale z obrázku sa nám vymazali mená vyznačených bodov. Dokresli do štvorčekovej siete celý štvorec KAMI.

Z4-I-5
Martin a Jana si porovnávali svoje Mikulášske balíčky. Mali tam nasypané aj svoje obľúbené čokoládky. Martin ich však mal iný počet ako Jana, tak venoval štvrtinu svojich čokoládok Jane. Jana si všetky svoje prepočítala a polovicu z nich venovala naspäť Martinovi. Potom Martin zase venoval štvrtinu svojich Jane. Po následnom prepočítaní zistili, že majú obaja po 9 čokoládok. Koľko čokoládok mal Martin pôvodne v balíčku? Koľko ich tam mala Jana? (Počas počítania a presúvania ani jednu čokoládku nezjedli.)

Z4-I-6
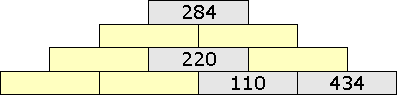
Doplň na prázdne tehličky pyramídy znázornenej na obrázku chýbajúce čísla tak, aby platilo: na každej tehličke (okrem tých z najspodnejšieho riadku) je napísané číslo, ktoré sa rovná polovici súčtu čísel napísaných na dvoch s ňou susediacich tehličkách z nižšieho riadku.

▲ hore ▲

Z4-II-1
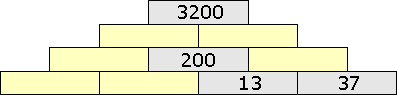
Doplň na prázdne tehličky pyramídy znázornenej na obrázku chýbajúce čísla tak, aby platilo: na každej tehličke (okrem tých z najspodnejšieho riadku) je napísané číslo, ktoré sa rovná dvojnásobku súčtu čísel napísaných na dvoch s ňou susediacich tehličkách z nižšieho riadku.

Z4-II-2
Z daných päťciferných čísel 53827 a 19763 vyškrtni spolu dve číslice tak, aby rozdiel vzniknutých čísel bol čo najmenší.

Z4-II-3
Martin narysoval obdĺžnik, ktorý sa dá bezo zvyšku rozstrihať na 3 štvorce. Aké rozmery mohol mať obdĺžnik, ak jeden zo štvorcov mal stranu dĺžky 7 cm? Vypočítaj jeho obvod.

▲ hore ▲

Z5-I-1
Náš kuchynský stôl má obdĺžnikovú vrchnú dosku s rozmermi 90 cm × 140 cm. Chceme naň ušiť obrus tak, aby na každej strane stola presahoval rovnako.

   a)  Koľko látky šírky 140 cm treba kúpiť, aby sme ju už nemuseli ďalej strihať?
   b)  Koľko cm bude tento obrus na každej strane presahovať?

Z5-I-2
Doplň na prázdne tehličky pyramídy znázornenej na obrázku chýbajúce čísla tak, aby platilo: na každej tehličke (okrem tých z najspodnejšieho riadku) je napísané číslo, ktoré sa rovná polovici súčtu čísel napísaných na dvoch s ňou susediacich tehličkách z nižšieho riadku.

Z5-I-3
V škôlke majú stavebnicu pozostávajúcu z rovnako veľkých molitanových kvádrov. Keď ich deti všetky položia na seba, poskladajú ich vždy tak, aby na sebe ležali kvádre rovnakými stenami a v žiadnom „poschodí“ neboli kvádre dva. Takto sa im postupne podarilo postaviť tri rôzne vysoké veže. Prvá mala 120 cm, druhá 150 cm a tretia 130 cm. Koľko kvádrov mohla mať stavebnica, z ktorej stavali?

Z5-I-4
Trojčatá práve oslávili svoje tretie narodeniny. O päť rokov bude súčet ich vekov rovný dnešnému veku ich mamy. Koľko rokov bude mať ich mama o 5 rokov?

Z5-I-5
Číslo sa nazýva PREFÍKANÉ, ak počnúc jeho treťou číslicou (počítané zľava) platí, že každá jeho číslica je súčtom všetkých číslic ležiacich naľavo od nej.

   a)  Napíšte dve najväčšie PREFÍKANÉ čísla.
   b)  Koľko je všetkých štvorciferných PREFÍKANÝCH čísel?

Z5-I-6
Doplň do prázdnych políčok prirodzené čísla od 1 do 16 (každé číslo môžeš použiť len raz) tak, aby platili matematické vzťahy.

▲ hore ▲

Z5-II-1
Polovica detí 5.A chodí na tanečný krúžok. Dievčatá chodia všetky a z osemnástich chlapcov chodí iba jedna tretina.

  a)  Koľko detí chodí do 5.A?
  b)  Koľko dievčat chodí do 5.A?

Z5-II-2
Majo sčítal štyri po sebe idúce dvojciferné čísla a súčet zaokrúhlil na desiatky. Juro vzal tie isté čísla, najprv ich zaokrúhlil na desiatky a potom ich sčítal. Jeho výsledok bol o 10 väčší ako Majov. Ktoré čísla sčítavali chlapci, ak ich výsledky neboli väčšie ako 100? Nájdi všetky možné riešenia.

Z5-II-3
Mamička šije utierky z látky šírky 120 cm. Hotová utierka má rozmery 60 cm × 38 cm. Pri strihaní látky treba počítať 2 cm naviac na každom okraji na začistenie. Najmenej koľko centimetrov tejto látky treba kúpiť, aby z nej mamičke vyšlo 10 utierok?

▲ hore ▲

Z6-I-1
Jurko kúpil dve čokolády v obchode oproti škole. Miško si kúpil také isté dve čokolády v obchode za školou a Ivan si kúpil tiež takú čokoládu, ale v školskom bufete. Spolu potom zistili, že priemerne ich spolu vyšla jedna čokoláda na 19,70 Sk. Takýmto spôsobom boli všetky tri nákupy spolu o 6 Sk drahšie, ako keby chlapci nakupovali všetkých 5 čokolád v obchode oproti škole a o 6,50 Sk lacnejšie, ako keby nakúpili iba v obchode za školou. Koľko stáli čokolády v jednotlivých obchodoch?

Z6-I-2
Miško mal farebné nálepky v tvare rovnoramenných pravouhlých trojuholníkov dvoch veľkostí. Prvý druh mal ramená dĺžky 5 cm, tých bolo 9. Druhý druh mal najdlhšiu stranu dĺžky 10 cm a týchto nálepiek bolo 17. Najmenej koľko nálepiek prvého druhu si má Miško ešte dokúpiť, aby svojimi nálepkami mohol úplne oblepiť (zakryť) steny kocky s hranou dĺžky 10 cm?

Z6-I-3
V rovine majú ležať body A, B, C, D tak, aby platilo: |AB| = 7 cm, |BC| = 8 cm, |CD| = 5 cm a |DA| = 9 cm.

   a)  Urči najväčšiu možnú vzdialenosť bodov A a C.
   b)  Urči najmenšiu možnú vzdialenosť bodov A a C.

Z6-I-4
Pri chudokrvnosti sa odporúča piť mrkvovo-cviklovú šťavu, pričom cviklová šťava má predstavovať len 1/5 z objemu nápoja. Z dvoch kg mrkvy získame v odšťavovači 7,5 dl šťavy, z jedného kg cvikly 6 dl šťavy.

   a)  Aké množstvo mrkvy potrebujeme na 25 dag cvikly, aby sme získali správne namiešanú mrkvovo-cviklovú šťavu?
   b)  Aké množstvo mrkvovo-cviklovej šťavy takto získame?

Z6-I-5
Ak povie mimozemšťan v rozhovore o Vianociach „haf quin lina“, znamená to „veľké zlaté hviezdy“; ak „kari lina mejk“, znamená to „blikajúce zlaté kolieska“; ak „esca haf kari“, znamená to „veľké červené kolieska“. Ako sa povie „blikajúce hviezdy“ ? (Zapíš svoju úvahu.)

Z6-I-6
Z trojciferných čísel 532 a 179 vyškrtni spolu dve číslice tak, aby súčin vzniknutých čísel bol čo najväčší.

▲ hore ▲

Z6-II-1
Na záhrade pána Kozla kvitlo niekoľko čerešní. Na každej čerešni sedeli tri škorce a ešte jeden sedel na plote. Pes pána Kozla ich vyplašil a škorce uleteli. Za chvíľu sa všetci vrátili a usadili sa opäť na čerešniach. Čerešňa, pod ktorou spal pes, zostala prázdna a na každej z ostatných sa usadili štyri škorce. Koľko čerešní má pán Kozel a koľko bolo na záhrade škorcov?

Z6-II-2
Daný je trojuholník ABC, v ktorom päta P kolmice z bodu C na priamku AB leží vo vnútri úsečky AB. Z bodu P sú vedené kolmice p, q na priamky AC a BC (v uvedenom poradí). Označme S priesečník priamky BC a priamky q a nech T je priesečník priamky AC a priamky p. Vypočítaj veľkosť uhla ACB, ak vieš, že |РAPT| + |РBPS| = 20°.

Z6-II-3
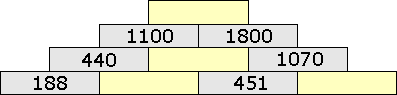
Na obrázku je zaokrúhľovacia sčítacia pyramída. Do každej tehličky (okrem tých z najspodnejšieho riadku) patrí súčet čísel napísaných na dvoch s ňou susediacich tehličkách z nižšieho riadku, ale príslušne zaokrúhlený: súčty v druhom riadku odspodu zaokrúhľujeme na desiatky, v treťom na stovky a v najvyššom štvrtom na tisíce. Doplňte do prázdnych tehličiek pyramídy najväčšie možné celé čísla.

▲ hore ▲

Z7-I-1
Číslo nazveme trochu nešťastné, ak je násobkom čísla 13. Číslo, ktoré je násobkom čísla 17, nazveme trochu usmievavé. Vezmime všetky prirodzené čísla od 1 do 1 000 000, ktoré nekončia ani 0 ani 5. Koľko z nich je trochu nešťastných a zároveň trochu usmievavých?

Z7-I-2
Vláda Tramtárie sa rozhodla, že svoje územie rozdelí na šesť krajov. Vybrala preto šesť najvýznamnejších miest (krajské mestá) a každému chce priradiť kraj podľa nasledujúceho pravidla: každé miesto v krajine patrí do kraja toho krajského mesta, ku ktorému to má vzdušnou čiarou najbližšie. Prekreslite si vo vhodnej mierke mapu Tramtárie a narysujte do nej hranice krajov.
(Krajské mestá sú označené písmenami A – F, hrubá čiara označuje hranice Tramtárie. Štvorcová sieť má iba uľahčovať orientáciu na mape a žiadnym spôsobom neovplyvňuje hranice krajov!)

Z7-I-3
O dvanástej stáli na parkovisku české, nemecké a francúzske autá v pomere: české k nemeckým 9:4, nemecké k francúzskym 2:3. V priebehu hodiny odišlo jedenásť a prišlo päť českých áut, odišlo jedno a prišlo jedenásť nemeckých áut a odišli tri a prišlo šesť francúzskych áut. Aký je pomer českých, nemeckých a francúzskych áut stojacich o 13:00 na parkovisku, ak o 12:00 tam bolo dvanásť francúzskych áut?

Z7-I-4
Úsečky AM, BM, CM a DM usporiadané ako na obrázku sú rovnakej dĺžky. Uhly, ktoré zvierajú, majú veľkosti 20°, 20°, 50°, 50°, 70° a a. Zisti veľkosť uhla, ktorý zvierajú priamky AB a CD.
(Obrázok je nepresný, nevyplatí sa ti merať.)

Z7-I-5
Všetky políčka na šachovnici 4×4 vyfarbite štyrmi rôznymi farbami a vpíšte do nich písmená L, E, T, O tak, aby v každom riadku aj v každom stĺpci boli zastúpené všetky farby aj všetky písmená. Každé políčko bude celé jednofarebné a bude obsahovať práve jedno písmeno.
Každé písmeno musí byť napísané na políčku každej farby a na každej farbe musia byť postupne umiestnené všetky písmená. Nájdi jedno riešenie.

Z7-I-6
Na papieri je napísaných niekoľko po sebe idúcich prirodzených čísel. Je medzi nimi 12 takých, ktoré sú násobkom piatich a 10 takých, ktoré sú násobkom siedmich.

   a)  Koľko prirodzených čísel je napísaných na papieri?
   b)  Nájdite jednu postupnosť prirodzených čísel, ktorá odpovedá vyššie opísaným podmienkam.

▲ hore ▲

Z7-II-1
Daný je rovnobežník ABCD (|AB| ¹ |BC|) s vnútorným uhlom veľkosti 72° pri vrchole A. Jedným vrcholom tohto rovnobežníka vedieme dve priamky, ktoré rozdeľujú rovnobežník na tri rovnoramenné trojuholníky. Určte veľkosti vnútorných uhlov týchto trojuholníkov.

Z7-II-2
Kráľ Lenivého kráľovstva vydal v nedeľu 1. apríla 2007 dekrét, ktorým vyradil zo všetkých nasledujúcich týždňov piatky. Od tej doby v jeho kráľovstve nasleduje vždy po štvrtku sobota a týždeň má iba šesť dní. Ktorý deň v týždni pripadne v Lenivom kráľovstve na 9. apríla 2008?
(Nezabudnite, že rok 2008 je priestupný!)

Z7-II-3
U Novákovcov napiekli svadobné koláče. Štvrtinu odviezli príbuzným na Moravu, šestinu rozdali kolegom v práci a devätinu dali susedom. Keby im zostali o tri koláče viacej, bola by to polovica pôvodného počtu. Koľko koláčov napiekli?

▲ hore ▲

Z8-I-1
Nájdite všetky štvorciferné čísla deliteľné tromi, ktoré po vynásobení číslom 17 dávajú číslo končiace trojčíslím 519.

Z8-I-2
Nájdite všetky trojice prirodzených čísel menších ako 10, pre ktoré platí, že ich súčin je sedemnásobok ich súčtu.

Z8-I-3
Jano si kúpil sedemmíľové čižmy. Jeho kamarát Honza z Čiech si kúpil lietajúci koberec. Potom sa obaja zúčastnili na rozprávkových 12-hodinových pretekoch. Počas pretekov boli hladní, a tak sa obaja zastavili najesť. Jedenie každému trvalo hodinu. Keby sa Honza nezastavil na „vepřo-knedlo-zelo“, predbehol by Jana o 51 rozprávkových míľ. Keby sa Jano nezastavil na bryndzové halušky, predbehol by Honzu o  28 rozprávkových míľ. Ako ďaleko od seba by skončili, keby nejedol ani jeden z nich? Kto z nich by bol prvý?

Z8-I-4
V Tramtárii majú 5 lekárskych fakúlt, z ktorých každá môže do prvého ročníka prijať presne 200 študentov. Prijímacie skúšky na jednotlivé fakulty sa konajú v rôzne dni, preto si študenti môžu podať prihlášku na viacero fakúlt. Pýtali sme sa na fakultách, koľko im prišlo prihlášok na školský rok 2007/2008. Získali sme tieto odpovede:

1. fakulta: „Dostali sme päťkrát viac prihlášok, ako sme mali voľných miest.“
2. fakulta: „U nás počet uchádzačov prevýšil kapacitu o 320%.“
3. fakulta: „Na našu fakultu sa hlásilo o 520 uchádzačov viac, ako sme mali miest.“
4. fakulta: „U nás na každé voľné miesto pripadli v priemere 3 prihlášky.“
5. fakulta: „K nám sa hlásilo o tri štvrtiny záujemcov viac, ako sme mali miest.“

V akademickom roku 2007/2008 nakoniec štúdium začalo 1000 medikov. Zo štatistiky vyplýva, že záujemca o štúdium medicíny podal na lekárske fakulty v priemere 2,5 prihlášky. Koľko záujemcov sa nedostalo na žiadnu z lekárskych fakúlt Tramtárie?

Z8-I-5
Pán Poleno a pán Čriepok vyrábali vchodové dvere tvaru obdĺžnika s obsahom 3 m². Rám, uhlopriečky a dve ďalšie priečky, ktoré spájali vrcholy obdĺžnika so stredmi protiľahlých strán boli z kovových tyčí (pozri obrázok). Pán Poleno vyplnil drevom štyri tmavé časti dverí a pán Čriepok zostávajúce časti dverí zasklil. Koľko metrov štvorcových dreva potreboval pán Poleno na výplň dverí?
(Hrúbku kovových tyčí zanedbajte.)

Z8-I-6
Uprostred námestia v Kocúrkove je štvorcový trávnatý záhon. Keď Kocúrkovčania zistili, že zabudli urobiť chodník, tak z každého kraja záhonu naň ubrali 2 metre. Pred položením zámkovej dlažby (a štrku pod ňu) bolo treba pod celú plochu chodníka urobiť 0,5 m hlboký výkop. Odkopaním trávy a hliny sa záhon zmenšil o 1200 m².

   a)  Aký obsah má teraz trávnatý záhon?
   b)  Koľko m³ štrku je pod dlažbou, ak je povrch dlažby zarovno s trávnatým záhonom a výška dlaždice je 8 cm?

▲ hore ▲

Z8-II-1
Družstvo chce v sezóne vyhrať všetkých svojich zápasov. V prvej tretine z nich však vyhralo iba 55% zápasov.

  a)  Koľko percent zvyšných zápasov by muselo družstvo vyhrať, aby dosiahlo zamýšľaný cieľ?
  b)  Keby družstvo vyhralo všetky zvyšné zápasy, koľko percent svojich zápasov by v celej sezóne vyhralo?

Z8-II-2
Akú časť obsahu nerovnoramenného lichobežníka KLMN (KL ║ MN) tvorí obsah trojuholníka ABC, kde A je stred základne KL, B je stred základne MN a C je stred ramena KN?

Z8-II-3
Aby prirodzené číslo prinášalo Liborovi šťastie, musí byť jeho druhá mocnina deliteľná číslami sedem, osem, deväť a desať. Nájdite všetky prirodzené čísla menšie ako 1000, ktoré Liborovi nosia šťastie.

▲ hore ▲

Z9-I-1
Nájdite všetky štvorciferné čísla končiace číslicou 9, ktoré sú deliteľné každou svojou číslicou.

Z9-I-2
Peter sa pýtal babičky, koľko rokov má dedko. Babička mu takto odpovedala: „To vieš, už dávno nemáme päťdesiat, ale zato ešte nemáme osemdesiat rokov. Ak vynásobíš súčet môjho a dedkovho veku ich rozdielom a k výsledku pripočítaš oba naše veky, dostaneš 492.“
„Aha,“ povedal po chvíli Peter, „tak to má dedko …“
Koľko rokov má Petrov dedko, ak viete, že je starší ako Petrova babička?

Z9-I-3
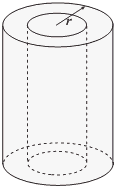
Stredom rotačného valca s výškou v a podstavou, ktorej polomer je r, bol vyvŕtaný valcový otvor. Objem takto vytvoreného „dutého valca“ je polovičný ako objem pôvodného valca. Vyjadrite hrúbku steny dutého valca pomocou polomeru r.

Z9-I-4
Minulú divadelnú sezónu sa predávali vstupenky za jednotnú cenu 160 Sk. Pre tohtoročnú sezónu sa sedadlá v hľadisku rozdelili do dvoch kategórií. Miesta I. kategórie stoja 180 Sk a miesta II. kategórie 155 Sk. Ak sa všetky sedadlá v hľadisku vypredajú, bude celková tržba rovnaká ako minulú sezónu pri vypredanom hľadisku. Riaditeľ divadla stále nie je spokojný a pre budúcu sezónu plánuje zmenu: z najhorších miest súčasnej II. kategórie urobí III. kategóriu. Aby sa však tržba za vypredané hľadisko nezmenila, tak rozhodol, že vstupenky budú stáť 180 Sk (I. kategória), 160 Sk (II. kategória) a 130 Sk (III. kategória). V akom pomere budú v budúcej sezóne počty sedadiel jednotlivých kategórií?

Z9-I-5
Jurko kúpil dve čokolády v obchode oproti škole. Miško si kúpil také isté dve čokolády v obchode za školou a Ivan si kúpil tiež takú čokoládu, ale v školskom bufete. Takýmto spôsobom boli všetky tri nákupy spolu o 6 Sk drahšie, ako keby chlapci nakupovali všetkých 5 čokolád v obchode oproti škole a o 6,50 Sk lacnejšie, ako keby nakúpili iba v obchode za školou. V školskom bufete predávajú jednu čokoládu za 19,50 Sk. Koľko stáli všetky čokolády spolu? Koľko stojí čokoláda v obchode za školou?

Z9-I-6
V rovine je daný štvoruholník ABCD. Zostrojte bod K, ktorý je vrcholom rovnobežníka BCDK, a bod L, ktorý je vrcholom rovnobežníka CDAL. Ukážte, že priamka KL prechádza stredom strany AB daného štvoruholníka ABCD.

▲ hore ▲

Z9-II-1
Barbora si napísala dve rôzne celé čísla. Potom ich sčítala, odčítala, vynásobila a vydelila. Dostala štyri výsledky, ktorých súčet bol -100. Keď vynechala výsledok sčítania a spočítala ostatné tri výsledky, dostala tiež súčet -100. Ktoré celé čísla mohla Barbora pôvodne napísať?

Z9-II-2
Z kociek o hrane 1 cm sme postavili kváder. Keby sme z kvádra odobrali jeden stĺpec (t.j. zvislý komínik), zvyšok stavby by sa skladal zo 602 kociek. Keby sme miesto toho odobrali jeden riadok hornej vrstvy, zostala by nám stavba zo 605 kociek. Aké rozmery má kváder?

Z9-II-3
Daný je štvorec ABCD so stranou dĺžky a a úsečka KL dĺžky 5a tak, že A ≡ K a strana AB leží na úsečke KL. Štvorec ABCD otočíme okolo pravého dolného bodu o pravý uhol a takéto otáčania robíme dovtedy, kým celá strana AB po prvý raz opäť nesplynie s časťou úsečky KL a bod B s bodom L.

  a)  Narysujte po akej dráhe sa bude pohybovať stred S strany AB.
  b)  Vypočítajte dĺžku krivky, po ktorej sa bod S pohyboval.

Z9-II-4
Severských pretekov psích záprahov sa zúčastnilo spolu 315 dvojzáprahov a trojzáprahov. Do cieľa dorazilo v stanovenom limite 60% všetkých dvojzáprahov a jedna tretina všetkých trojzáprahov, čo predstavovalo polovicu všetkých psov na štarte. Koľko dvojzáprahov a koľko trojzáprahov štartovalo?

▲ hore ▲

Z9-III-1
V Dlhej Lehote volili starostu. Kandidovali dvaja občania: Ing. Schopný a jeho manželka Dr. Schopná. V obci boli tri volebné miestnosti. V prvej i druhej miestnosti dostala viac hlasov Dr. Schopná. V prvej bol pomer hlasov 7:5, v druhej 5:3. V tretej volebnej miestnosti bol pomer hlasov 3:7 v prospech Ing. Schopného. Voľby nakoniec skončili nerozhodne, obaja kandidáti totiž získali rovnaký počet hlasov. V akom pomere boli počty odovzdaných platných hlasovacích lístkov v jednotlivých volebných miestnostiach, ak vieme, že v prvej a druhej miestnosti odovzdal platný hlas rovnaký počet občanov?

Z9-III-2
Je daný rovnoramenný lichobežník ABCD (AB║CD), kde |AB| > |CD|. Bodom A sa dajú viesť dve priamky tak, aby rozdelili lichobežník na tri rovnoramenné trojuholníky. Určite veľkosti uhlov lichobežníka ABCD.

Z9-III-3
Nájdite všetky prirodzené čísla x, y, pre ktoré platí:

1 + x + y + xy = 2008.

Z9-III-4
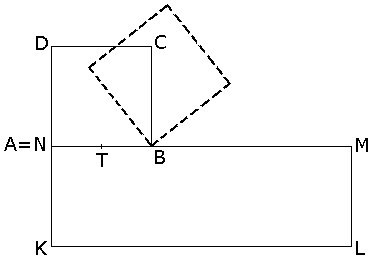
Daný je štvorec ABCD so stranou dĺžky a a obdĺžnik KLMN so stranami dĺžok |KL| = 3a a |LM| = a. Na začiatku je štvorec umiestnený tak, že A ≡ N a strana AB leží na strane NM. Štvorec ABCD otočíme okolo bodu B tak, že strana BC bude ležať na strane MN. Štvorec sa otáčaním okolo svojich vrcholov (pozri obrázok) pohybuje po obvode obdĺžnika KLMN tak dlho, až sa opäť dostane do svojej pôvodnej polohy.

  a)   Narysujte dráhu, po ktorej sa bude pohybovať bod T, ktorý je stredom strany AB.
  b)   Určte obsah plochy ohraničenej krivkou, ktorú opisuje bod T.

▲ hore ▲