68. ročník matematickej olympiády 2018-2019
Súťažné úlohy kategórií Z5-Z9
aktualizované 30.1.2020 10:25
| Z5 | Z6 | Z7 | Z8 | Z9 |
| domáce | domáce | domáce | domáce | domáce |
| obvodné | obvodné | obvodné | obvodné | obvodné |
| krajské | ||||
Z5-I-1
Miška má päť pasteliek. Vojto ich má menej ako Miška. Vendelín ich má toľko, koľko Miška a Vojto spolu. Všetci traja spolu majú sedemkrát viac pasteliek, ako má Vojto. Koľko pasteliek má Vendelín?
Z5-I-2
Tereza dostala štyri zhodné pravouhlé trojuholníky so stranami dĺžok 3 cm, 4 cm a 5 cm. Z týchto trojuholníkov (nie nutne zo všetkých štyroch) skúšala skladať nové útvary. Postupne sa jej podarilo zložiť štvoruholníky s obvodom 14 cm, 18 cm, 22 cm a 26 cm, a to zakaždým dvoma rôznymi spôsobmi (t. j. tak, že žiadne dva štvoruholníky neboli zhodné). Nakreslite, aké štvoruholníky mohla Tereza zložiť.
Z5-I-3
Štefka rada oslavuje, takže okrem narodenín vymyslela ešte antinarodeniny: dátum antinarodenín vznikne tak, že sa vymení číslo dňa a číslo mesiaca v dátume narodenia. Sama sa narodila 8.11., takže antinarodeniny má 11.8. Jej mamička antinarodeniny oslavovať nemôže: narodila sa 23.7., jej antinarodeniny by mali byť 7.23., čo ale nie je dátum žiadneho dňa v roku. Jej brat síce antinarodeniny oslavovať môže, ale má ich v ten istý deň ako narodeniny: narodil sa 3.3. Koľko dní v roku je takých, že človek, ktorý sa toho dňa narodil, môže oslavovať svoje antinarodeniny, a to v iný deň ako svoje narodeniny?
Z5-I-4
V novej klubovni boli iba stoličky a stôl. Každá stolička mala štyri nohy, stôl bol trojnohý. Do klubovne prišli skauti. Každý si sadol na svoju stoličku, dve stoličky zostali neobsadené a počet nôh v miestnosti bol 101. Určte, koľko stoličiek bolo v klubovni.
Z5-I-5
Tomáš dostal deväť kartičiek, na ktorých boli nasledujúce čísla a matematické symboly:
Kartičky ukladal tak, že vedľa seba nikdy neležali dve kartičky s číslami, t. j. striedali sa kartičky s číslami a kartičky so symbolmi. Takto vzniknuté úlohy vypočítal a výsledok si zapísal. Určte, aký najväčší výsledok mohol Tomáš získať.
Z5-I-6
Na obrázku je hrací plánik a cesta, ktorú Juro zamýšľal prejsť z pravého dolného rohu do ľavého horného. Potom zistil, že má plánik chybne pootočený, teda že by nezačínal v pravom dolnom rohu. Tvar zamýšľanej cesty už ale nemohol zmeniť a musel ju prejsť pri správnom natočení plánika. Pre každé z troch možných natočení prekreslite uvedenú cestu a určte, koľkými sivými políčkami táto cesta prechádza.

|
|
 |
Z5-II-1
Pretekov chrtov sa zúčastnilo 36 psov. Počet psov, ktoré do cieľa dobehli pred Dunčom, bol štyrikrát menší ako počet tých, ktoré dobehli za ním. Koľký bol Dunčo?
Z5-II-2
Agáta napísala dvadsaťciferné číslo 12345678901234567890. Filip si z Agátinho čísla vybral štyri cifry, ktoré boli zapísané bezprostredne za sebou. Tieto štyri cifry skúšal zapísať v rôznom poradí a nakoniec sa mu z nich podarilo zostaviť dvojicu dvojciferných čísel, z ktorých prvé bolo o 1 väčšie ako druhé. Ktoré dvojice čísel mohol Filip zostaviť? Určte všetky možnosti.
Z5-II-3
Anička vyrazila z hotela na prechádzku, išla 5 km na sever, potom 2 km na východ, 3 km na juh a nakoniec 4 km na západ. Tak došla k rybníku, kde sa okúpala. Vojto vyšiel z kempu, išiel 3 km na juh, 4 km na západ a 1 km na sever. Tak došiel ku skale, ktorá bola 5 km západne od rybníka, v ktorom sa kúpala Anička. Inokedy vyšla Anička zo svojho hotela a Vojto zo svojho kempu, obaja chceli dôjsť k rybníku, v ktorom sa predtým kúpala Anička, a obaja postupovali iba v smeroch štyroch svetových strán. Určte, koľko najmenej kilometrov musela prejsť Anička a koľko Vojto.
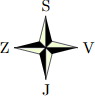
|
|
 |
Z6-I-1
Ivan a Mirka sa delili o hrušky v mise. Ivan si vždy berie dve hrušky a Mirka polovicu toho, čo v mise ostáva. Takto postupne odoberali Ivan, Mirka, Ivan, Mirka a nakoniec Ivan, ktorý vzal posledné dve hrušky. Určte, kto mal nakoniec viac hrušiek a o koľko.
Z6-I-2
Ernest si zo štvorčekového papiera vystrihol štvorec 4 × 4. Kristián v ňom vystrihol dve diery, pozri dva čierne štvorčeky na obrázku. Tento útvar skúšal Ernest rozstrihnúť podľa vyznačených čiar na dve zhodné časti. Nájdite aspoň štyri rôzne spôsoby, ako to mohol Ernest spraviť. (Pritom dve strihania považujte za rôzne, ak časti vzniknuté jedným strihaním nie sú zhodné s časťami vzniknutými druhým strihaním.)

Z6-I-3
Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplnte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch susediacich políčkach bol 2018. Určte číslo, ktoré bude v 2019. políčku v hornom rade.
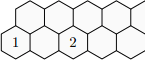
Z6-I-4
Pán Ticháček mal na záhrade troch sadrových trpaslíkov: najväčšieho volal Maško, prostredného Jarko a najmenšieho Fanko. Keďže sa s nimi rád hrával, časom zistil, že keď postaví Fanka na Jarka, sú rovnako vysokí ako Maško. Keď naopak postaví Fanka na Maška, merajú spolu o 34 cm viac ako Jarko. A keď postaví na Maška Jarka, sú o 72 cm vyšší ako Fanko. Ako vysokí sú trpaslíci pána Ticháčka?
Z6-I-5
V nasledujúcom príklade na s4ítanie predstavujú rovnaké písmená rovnaké cifry, rôzne písmená rôzne cifry:
| R | A | T | A | M |
| R | A | D | ||
| U | L | O | H | Y |
Nahraďte písmená ciframi tak, aby bol príklad správne. Nájdite dve rôzne nahradenia.
Z6-I-6
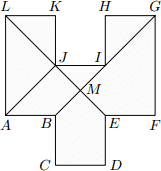
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M a rozdeľujú dvanásťuholník na šesť útvarov (tri trojuholníky, dva štvoruholníky a jeden päťuholník). Štvoruholník EFGM má obsah 7 cm2. Určte obsahy ostatných piatich útvarov.
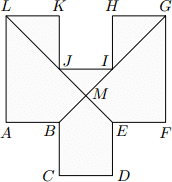
|
|
 |
Z6-II-1
Jano, Dano, Anna a Hana majú každý svoje obľúbené číslo. Vieme, že
- keď sčítame Danovo číslo a trojnásobok Janovho čísla, vyjde nepárne číslo,
- keď odčítame od seba Annino a Hanino číslo a tento výsledok vynásobíme piatimi, vyjde nepárne číslo,
- keď vynásobíme Danovo číslo Haniným číslom a k výsledku pripočítame 17, vyjde párne číslo.
Určte, čie obľúbené čísla sú nepárne a čie párne.
Z6-II-2
Anička má v kasičke našporených 290 mincí, a to jednoeurovky a dvojeurovky. Keď použije štvrtinu všetkých dvojeuroviek, zloží rovnakú sumu, ako keď použije tretinu všetkých jednoeuroviek. Akú sumu má Anička našporenú?
Z6-II-3
Útvar na obrázku je zložený z piatich zhodných štvorcov a je rozdelený úsečkami na tri farebne odlíšené časti. Obsah sivej časti je o 0,6 cm2 väčší ako obsah bielej časti. Určte obsah celého útvaru.
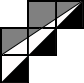
|
|
 |
Z7-I-1
Na každej z troch kartičiek je napísaná jedna cifra rôzna od nuly (na rôznych kartičkách nie sú nutne rôzne cifry). Vieme, ¾e akékoľvek trojciferné číslo zložené z týchto kartičiek je deliteľné šiestimi. Navyše možno z týchto kartičiek zložiť trojciferné číslo deliteľné jedenástimi. Aké cifry môžu byť na kartičkách? Určte všetky možnosti.
Z7-I-2
V dvanásťuholníku ABCDEFGHIJKL sú každé dve susedné strany navzájom kolmé a všetky strany s výnimkou strán AL a GF sú navzájom zhodné. Strany AL a GF sú oproti ostatným stranám dvojnásobne dlhé. Úsečky BG a EL sa pretínajú v bode M. Štvoruholník ABMJ má obsah 1,8 cm2. Určte obsah štvoruholníka EFGM.
Z7-I-3
Dedo pripravil pre svojich šesť vnúčat kôpku lieskových orieškov s tým, nech si ich nejako rozoberú. Prvý prišiel Adam, odpočítal si polovicu, pribral si ešte jeden oriešok a odišiel. Rovnako sa zachoval druhý Bob, tretí Cyril, štvrtý Dano aj piaty Edo. Iba Ferko smutne hľadel na prázdny stôl, už pre neho žiadny oriešok nezvýšil. Koľko orieškov bolo pôvodne na kôpke?
Z7-I-4
Betka sa hrala s ozubenými kolesami, ktoré ukladala tak, ako je naznačené na obrázku. Keď potom zatočila jedným okolo, točili sa všetky ostatné. Nakoniec bola spokojná so súkolesím, pričom prvé koleso malo 32 a druhé 24 zubov. Keď sa tretie koleso otočilo presne osemkrát, druhé koleso urobilo päť otáčok a časť šiestej a prvé koleso urobilo štyri otáčky a časť piatej. Zistite, koľko zubov malo tretie koleso.

Z7-I-5
V záhradníctve Rose si jedna predajňa objednala celkom 120 ruží vo farbe červenej a žltej, druhá predajňa celkom 105 ruží vo farbe červenej a bielej a tretia predajňa celkom 45 ruží vo farbe žltej a bielej. Záhradníctvo zákazku splnilo, a to tak, že ruží rovnakej farby dodalo do každého obchodu rovnako. Koľko celkom červených, koľko bielych a koľko žltých ruží dodalo záhradníctvo do týchto troch predajní?
Z7-I-6
Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostrojte.
|
|
 |
Z7-II-1
Majka, Vašo a Zuzka počítali cez víkend úlohy. Majka a Vašo vypočítali dokopy 25 úloh. Zuzka a Vašo vypočítali dokopy 32 úloh. Pritom Zuzka vypočítala dvakrát viac úloh ako Majka. Koľko úloh vypočítal Vašo?
Z7-II-2
Medzi cifry čísla 2019 vložte dve cifry tak, aby vzniknuté šesťciferné číslo
- začínalo 2 a končilo 9,
- bolo zložené zo šiestich rôznych cifier,
- bolo deliteľné tromi,
- jeho prvé trojčíslie bolo deliteľné tromi,
- jeho prvé štvorčíslie bolo deliteľné štyrmi,
- súčet vložených cifier bol nepárny.
Určte rozdiel najväčšieho a najmenšieho šesťciferného čísla s uvedenými vlastnosťami.
Z7-II-3
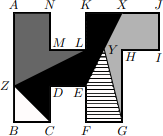
Útvar na obrázku je zložený z ôsmich zhodných štvorcov a je rozdelený úsečkami na päť farebne odlíšených častí. Pritom bod X je stredom úsečky KJ, bod Y je stredom úsečky EX a úsečka BZ je zhodná s BC. Obsah čiernej časti útvaru je 7,5 cm2. Určte obsahy zvyšných štyroch častí.
|
|
 |
Z8-I-1
Fero a Dávid sa denne stretávajú vo výťahu. Raz ráno zistili, že keď vynásobia svoje súčasné veky, dostanú 238. Keby to isté urobili za štyri roky, bol by tento súčin 378. Určte súčet súčasných vekov Fera a Dávida.
Z8-I-2
Do triedy pribudol nový žiak, o ktorom sa vedelo, že okrem angličtiny vie výborne ešte jeden cudzí jazyk. Traja spolužiaci sa dohadovali, ktorý jazyk to je.
Prvý súdil: „Francúzština to nie je.“
Druhý hádal: „Je to španielčina alebo nemčina.“
Tretí usudzoval: „Je to španielčina.“
Vzápätí sa dozvedeli, že aspoň jeden z nich hádal správne a aspoň jeden nesprávne. Určte, ktorý z menovaných jazykov nový žiak ovládal.
Z8-I-3
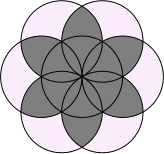
Peter narysoval pravidelný šesťuholník, ktorého vrcholy ležali na kružnici dĺžky 16 cm. Potom pre každý vrchol tohto šesťuholníka narysoval kružnicu so stredom v tomto vrchole, ktorá prechádzala jeho dvoma susednými vrcholmi. Vznikol tak útvar ako na obrázku. Určte obvod vyznačeného kvietka.
Z8-I-4
Na štyroch kartičkách boli štyri rôzne cifry, z ktorých jedna bola nula. Vojto z kartičiek zložil čo najväčšie štvorciferné číslo, Martin potom čo najmenšie štvorciferné číslo. Adam zapísal na tabuľu rozdiel Vojtovho a Martinovho čísla. Potom Vojto z kartičiek zložil čo najväčšie trojciferné číslo a Martin čo najmenšie trojciferné číslo. Adam opäť zapísal na tabuľu rozdiel Vojtovho a Martinovho čísla. Potom Vojto s Martinom podobne zložili dvojciferné čísla a Adam zapísal na tabuľu ich rozdiel. Nakoniec Vojto vybral čo najväčšie jednociferné číslo a Martin čo najmenšie nenulové jednociferné číslo a Adam zapísal ich rozdiel. Keď Adam sčítal všetky štyri rozdiely na tabuli, vyšlo mu 9090. Určte štyri cifry na kartičkách.
Z8-I-5
Kráľ dal murárovi Václavovi za úlohu postaviť múr silný 25 cm, dlhý 50 m a vysoký 2 m. Ak by Václav pracoval bez prestávky a rovnakým tempom, postavil by múr za 26 hodín. Podľa platných kráľovských nariadení však musí Václav dodržiavať nasledujúce podmienky:
- Počas práce musí spraviť práve šesť polhodinových prestávok.
- Na začiatku práce a po každej polhodinovej prestávke, keď je dostatočne oddýchnutý, môže pracovať o štvrtinu rýchlejšie ako normálnym tempom, ale nie dlhšie ako jednu hodinu.
- Medzi prestávkami musí pracovať najmenej 3/4 hodiny.
Za aký najkratší čas môže Václav splniť zadanú úlohu?
Z8-I-6
V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má veľkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP.
|
|
 |
Z8-II-1
V dvojposchodovom dome, ktorý má obytnú časť okrem 1. a 2. poschodia aj na prízemí, býva 35 ľudí nad niekým a 45 ľudí býva pod niekým. Pritom na 1. poschodí býva jedna tretina všetkých osôb žijúcich v dome. Koľko osôb býva v dome celkom?
Z8-II-2
Pre koľko kladných celých čísel menších ako 1000 platí, že medzi číslami 2, 3, 4, 5, 6, 7, 8 a 9 je práve jedno, ktoré nie je jeho deliteľom?
Z8-II-3
V lichobežníku ABCD so základňami AB a CD platí, že |AD| = |CD|, |AB| = 2|CD|, |BC| = 24 cm a |AC| = 10 cm. Vypočítajte obsah lichobežníka ABCD.
|
|
 |
Z9-I-1
Nájdite všetky kladné celé čísla x a y, pre ktoré platí
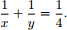
Z9-I-2
V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
Z9-I-3
V našom meste sú štyri kiná, ktorým sa hovorí podľa svetových strán. O ich otváracích hodinách je známe, že:
- každý deň je otvorené aspoň jedno kino,
- ak je otvorené južné kino, tak nie je otvorené severné kino,
- nikdy nie je otvorené súčasne severné a východné kino,
- ak je otvorené východné kino, tak je otvorené aj južné alebo severné kino (alebo obe).
Vydali sme sa do južného kina a zistili sme, že je zatvorené. Ktoré zo zvyšných kín je určite otvorené?
Z9-I-4
Hotelier chcel vybaviť jedáleň novými stoličkami. V katalógu si vybral typ stoličky. Až pri zadávaní objednávky sa od výrobcu dozvedel, že v rámci zľavovej akcie ponúkajú každú štvrtú stoličku za polovičnú cenu a že teda oproti plánu môže ušetriť za sedem a pol stoličky. Hotelier si spočítal, že za pôvodne plánovanú čiastku môže zaobstarať o deväť stoličiek viac, ako zamýšľal. Koľko stoličiek chcel hotelier pôvodne kúpiť?
Z9-I-5
Adam a Eva vytvárali dekorácie z navzájom zhodných bielych kruhov. Adam použil štyri kruhy, ktoré položil tak, že sa každý dotýkal dvoch iných kruhov. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých štyroch bielych kruhov, a ten vyfarbil červenou. Eva použila tri kruhy, ktoré položila tak, že sa dotýkali navzájom. Medzi ne potom vložila iný kruh, ktorý sa dotýkal všetkých troch bielych kruhov, a ten vyfarbila zelenou. Eva si všimla, že jej zelený kruh a Adamov červený kruh sú rôzne veľké, a začali spolu zisťovať, ako sa líšia. Vyjadrite polomery červeného a zeleného kruhu všeobecne pomocou polomeru bielych kruhov.
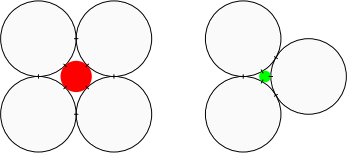
Z9-I-6
Prirodzené číslo N nazveme bombastické, ak neobsahuje vo svojom zápise žiadnu nulu a ak žiadne menšie prirodzené číslo nemá rovnaký súčin cifier ako číslo N. Karol sa najskôr zaujímal o bombastické prvočísla a tvrdil, že ich nie je veľa. Vypíšte všetky dvojciferné bombastické prvočísla. Potom Karol zvolil jedno bombastické číslo a prezradil nám, že obsahuje cifru 3 a že iba jedna z jeho ďalších cifier je párna. O ktorú párnu cifru sa mohlo jednať?
|
|
 |
Z9-II-1
Marienka napísala na tabuľu dve rôzne prirodzené čísla. Marta si vzala kartičku, na ktorej jednu stranu napísala súčet Marienkiných čísel a na druhú stranu ich súčin. Jedno z čísel na kartičke bolo prvočíslo a súčet čísel z oboch strán kartičky bol 97. Ktoré čísla napísala Marienka na tabuľu?
Z9-II-2
Máme kváder, ktorého jedna hrana je päťkrát dlhšia ako iná jeho hrana. Keby sme výšku kvádra zväčšili o 2 cm, zväčšil by sa jeho objem o 90 cm3. Keby sme výšku takto zväčšeného kvádra zmenili na polovicu, bol by objem nového kvádra rovný trom pätinám objemu pôvodného kvádra. Aké môžu byť rozmery pôvodného kvádra? Určte všetky možnosti.
Z9-II-3
Z cifier 3, 4, 5, 7 a 9 boli vytvorené všetky možné trojciferné čísla tak, aby sa každá cifra vyskytovala v každom čísle nanajvýš raz. Určte počet takto vzniknutých čísel a ich celkový súčet.
Z9-II-4
V pravouhlom trojuholníku je polomer jemu opísanej kružnice 14,5 cm a polomer jemu vpísanej kružnice 6 cm. Určte obvod tohto trojuholníka.
|
|
 |
Z9-III-1
Adela napísala na tabuľu dve kladné celé čísla a dala Lukášovi a Petrovi za úlohu určiť kladný rozdiel druhých mocnín týchto dvoch čísel. Lukáš namiesto toho určil druhú mocninu rozdielu daných dvoch čísel. Vyšlo mu tak číslo o 4 038 menšie ako Petrovi, ktorý výpočet vykonal správne. Ktoré dve čísla mohla Adela napísať na tabuľu? Určte všetky možnosti.
Z9-III-2
Na ostrove žijú dva druhy domorodcov: Poctivci, ktorí vždy hovoria pravdu, a Klamári, ktorí vždy klamú. Keď cudzinec stretol troch domorodcov, Alana, Bruna a Ctibora, spýtal sa ich, do ktorej skupiny patria.
Alan oznámil: ”Bruno je Klamár.“
Bruno povedal: ”Alan a Ctibor sú buď obaja Klamári, alebo obaja Poctivci.“
Ctibor sa nevyjadril.
Mohol cudzinec pri niektorom z týchto domorodcov s istotou určiť, či je Poctivec, alebo Klamár?
Z9-III-3
Keď číslo X vydelím číslom Y, dostanem číslo Z a zvyšok 27. Keď číslo X vydelím číslom Z, dostanem číslo 1,1 · Y a zvyšok 3. Ktoré čísla X, Y, Z vyhovujú uvedeným podmienkam? Určte všetky možnosti.
Z9-III-4
Daná je kružnica so stredom S a polomerom 39 mm. Do kružnice máme vpísať trojuholník ABC tak, aby veľkosť strany AC bola 72 mm a bod B ležal v polrovine určenej priamkou AC a bodom S. Zo zadaných údajov vypočítajte, akú veľkosť má mať výška trojuholníka ABC z vrcholu B, aby úloha mala dve riešenia.
|
|
 |
