51. ročník matematickej olympiády 2001-2002
Súťažné úlohy kategórií Z4-Z9

aktualizované 25.2.2019 23:25

Z4	Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce	domáce
domáce	obvodné	obvodné	obvodné	obvodné	obvodné
					krajské

 

Z4-I-1
Anička má našetrených 129 Sk, 72 Sk však dlhuje Borisovi. Dávid si našetril 145 Sk, ale 76 Sk dlhuje Aničke. Boris má našetrených 163 Sk a 89 Sk dlhuje Dávidovi. Ktoré z detí bude mať najviac korún, keď sa vyrovnajú všetky dlžoby? Koľko to bude?

Z4-I-2
Z papiera sme vystrihli všetky obdĺžniky, ktoré sa dajú poskladať zo štvorčekov 1 cm x 1 cm a ktorých obvody sú menšie ako 13 cm. Narysuj najväčší štvorec, ktorý môžeme zložiť z vystrihnutých obdĺžnikov. Obdĺžniky sa nesmú prekrývať, nemusíme ale pri skladaní použiť všetky.

Z4-I-3
V škole riešili štvrtáci takúto úlohu: „Myslím si číslo. Ak ho vynásobím 5 a k tomuto násobku pripočítam číslo 6, vyjde mi číslo 11. Aké číslo si myslím?“ Za domácu úlohu potom dostali vyriešiť „tú istú“ úlohu „Myslím si číslo. Ak ho vynásobím … a k tomuto násobku pripočítam …, vyjde mi číslo … Aké číslo si myslím?“, ale s číslami 8, 23 a 5.Vyrieš „školskú úlohu“.
Napíš, ako vyzeralo zadanie domácej úlohy, ak vieš, že mala riešenie a vyrieš ju.

Z4-I-4
Vpíšte do trojuholníkov na obrázku čísla tak, aby aspoň v jednom trojuholníku bolo číslo 279, súčet vpísaných čísel bol v každom kosoštvorci zloženom z dvoch trojuholníkov ten istý, súčet všetkých vpísaných čísel bol 4200.

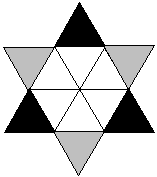
Z4-I-5
Včera som v našej záhrade narátala 136 lienok. Každá z nich mala dve, šesť alebo sedem bodiek. Všetky dvojbodkové lienky mali spolu toľko bodiek ako všetky šesťbodkové. Všetky šesťbodkové mali spolu rovnako veľa bodiek ako všetky sedembodkové. Koľko akých lienok som videla v záhrade?

Z4-I-6
Do 4.A chodí 27 žiakov. Šiesti z nich sú jedináčikovia, dvanásti majú mladšieho súrodenca, šestnásti staršieho súrodenca, z dvojičiek, trojičiek ani iných „viac-ičiek“ nie je nik. Koľko detí tejto triedy nemá mladšieho súrodenca? Koľkí majú len jedného súrodenca?

Z4-II-1
Vpíšte do šedých trojuholníčkov na obrázku čísla tak, aby súčet čísel vpísaných do ľubovoľných dvoch šedých trojuholníčkov so spoločným vrcholom bol 238.

Z4-II-2
Majka, Vojto a Peťo sa hrali guľky. Na začiatku hry mala Majka o 6 guliek menej ako Peťo a o 7 viac ako Vojto. Na konci hry mal Vojto o 8 guliek menej ako Majka a o 9 viac ako Peťo. Zistite, koľko guliek mala Majka na začiatku, ak ich na konci hry mala 20..

Z4-II-3
Riško vystrihol z papiera obdĺžnik, ktorý sa dá poskladať zo štvorčekov 1 cm × 1 cm a ktorého obvod je 18 cm. Potom vystrihol z papiera ešte niekoľko štvorčekov 1cm × 1cm. Z obdĺžnika a všetkých štvorčekov zložil veľký štvorec s obvodom 24 cm. Koľko najmenej štvorčekov vystrihol Riško?
(Pri skladaní sa obdĺžnik a štvorce nesmú prekrývať a musíme všetky použiť.)

Z5-I-1
Pavol má v stavebnici drevené kocky a kvádre. Hrana každej kocky meria 3 cm. Každý kváder má rozmery 5 cm, 5 cm, 7 cm. Z celej stavebnice postavil Pavol vežu vysokú 50 cm. Koľko najmenej dielov môže mať v stavebnici? Koľko najviac ich môže mať? (Vežu stavia tak, že v každej vrstve je buď len 1 kocka alebo len 1 kváder.)

Z5-I-2
Plamienkovci vyrábajú sviečky pre celé Svetielkovo. Vosk roztopia vo veľkom hrnci a všetok vylejú do pripravených foriem. Z každej formy vyberú 5 sviečok a očistením formy od zvyškov vosku získajú materiál na výrobu ešte 1 sviečky. Všetky zvyšky spolu roztopia a rovnako ako predtým vyrábajú ďalšie sviečky. Tento postup opakujú dovtedy, kým sa dá voskom naplniť celá forma. Pri minutí všetkého vosku z prvého roztápania vyrobili Plamienkovci 360 sviečok. Koľko sviečok vyrobili pri druhom roztápaní? Koľko sviečok vyrobili celkom?

Z5-I-3
Pestré číslo je také, ktoré nemé žiadne dve cifry rovnaké. Zrkadlovým obrazom čísla 102 958 je číslo 859 201. Aký najmenší a aký najväčší 5-ciferný výsledok môžeme dostať pri správnom sčítaní dvoch pestrých štvorciferných čísel, z ktorých jedno je zrkadlovým obrazom druhého?

Z5-I-4
Za prekročenie rýchlosti dávajú v Slowlande veľké pokuty. Za každý km/h navy3e oproti maximálnej povolenej rýchlosti zaplatíte 400 Sk. Polícia zastavila pána Quicka a povedala mu: „Išli ste rýchlosťou 93 km/h. Keby ste išli ešte o 7 km/h rýchlejšie, zaplatili by ste pokutu 18 000 Sk.“

    a) Aká je maximálna povolená rýchlosť v Slowlande?
    b) Koľko zaplatil pán Quick za prekročenie rýchlosti?

Z5-I-5
Na obrázku sú znázornené všetky vrcholy dvoch štvorcov. Zisti obsah ich spoločnej časti. (Jeden štvorček siete má obsah 25 mm².)

Z5-I-6
Tramtárijské vlaky majú ružové a modré vagóniky, ktoré musia byť zoradené tak, aby žiadne dva vagóniky rovnakej farby neboli vedľa seba. Nový zoraďovač to nevedel a za lokomotívu zaradil najprv 5 ružových a potom 5 modrých vagónov.
V akom najkratšom čase to teraz môže napraviť, ak vie na pomocnej koľaji vymeniť poradie dvoch susedných vagónov a jedna takáto výmena mu trvá 10 minút?

Z5-II-1
Pestré číslo je také, ktoré nemá žiadne dve cifry rovnaké. Zrkadlovým obrazom pestrého čísla 102 958 je číslo 859 201. Myslím si dve dvojciferné čísla. Obe sú pestré a jedno je zrkadlovým obrazom druhého. Ich súčin je trojciferné číslo a nie je pestré. Aké čísla si môžem myslieť? Je viac možností?

Z5-II-2
47-hlavá dračica bola nakupovať. Pre každú svoju hlavu kúpila v akcii 1 šál po 50 Sk, 1 čiapku po 40 Sk, 1 kefku na zuby po 30 Sk, 1 hrebeň po 20 Sk, a 1 mašľu po 10 Sk. Pri pokladni jej naúčtovali 7 000 Sk a dračica hneď vedela, že sa museli pomýliť. A naozaj, pri kontrole zistila, že jej naúčtovali 1 hrebeň a 1 šál navyše, zato 4 rovnaké veci zarátať zabudli.

    a) Koľko mala dračica správne zaplatiť?
    b) Čo jej zabudli zarátať?

Z5-II-3
Na obrázku sú znázornené všetky vrcholy dvoch štvorcov. Vypočítajte obsah spoločnej časti týchto dvoch štvorcov. (Strana štvorčeka siete meria 5 mm.)

Z6-I-1
Moja mama sa narodila 16.3. 1948. Je to pekný dátum, platí totiž 16 x 3 = 48. V ktorých rokoch 20. storočia bolo najmenej takých pekných dátumov? Nájdite všetky riešenia.

Z6-I-2
Dominik sa hral s plastelínou a vymodeloval kváder s rozmermi 6 cm x 3 cm x 19 cm. Potom ho znova roztlačil a z tejto plastelíny vymodeloval tri rôzne veľké kocky. Na svoje prekvapenie zistil, že veľkosti všetkých hrán v centimetroch boli celé čísla. Aké rozmery mali Dominikove kocky?

Z6-I-3
Prirodzené číslo je veselé, ak je deliteľné 9 alebo 13, smutné, ak je deliteľné 12, hladné, ak obsahuje aspoň jednu nulu, malé, ak je dvojciferné a veľké, ak je trojciferné menšie než 200. Ako veľký obsah môže mať obdĺžnik, ktorého šírka je malá, smutná, hladná a dĺžka je veľká, veselá, hladná a jeho obvod je tiež hladný?

Z6-I-4
Doplň do „súčinovej pyramídy“ na obrázku prirodzené čísla tak, aby najväčšie doplnené číslo bolo 315 a žiadne dve doplnené čísla neboli rovnaké. Koľkými rôznymi spôsobmi sa to dá spraviť?

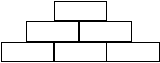
Z6-I-5
Ivan dostal špeciálnu bielo-hnedú čokoládu ako na obrázku. Zisti hmotnosť bielej časti, ak celá čokoláda má tri rovnako široké riadky a tri rovnako široké stĺpce a celá váži 144 gramov.

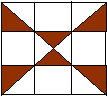
Z6-I-6
Traja dalmatínci a 2 špici vážia toľko ako 14 jazvečíkov. Jeden dalmatínec váži toľko ako 1 špic a 3 jazvečíci. Koľko jazvečíkov vyváži 101 dalmatíncov? (Psi jedného plemena sú vždy rovnako ťažkí.)

Z6-II-1
Ferko sa rozhodol minúť všetky svoje úspory na maškrty. Zistil, že si za ne môže kúpiť 3 veterníky a 3 dl čapovanej kofoly, alebo 18 dekagramov hrozienok v jogurte, prípadne 12 dekagramov hrozienok v jogurte a pol litra kofoly. Nakoniec si kúpil 1 veterník a 6 dl kofoly. Na koľko gramov hrozienok v jogurte mu ešte zvýšili peniaze?

Z6-II-2
Katka rozstrihla štvorcovú šatku nakreslenú na obrázku pozdĺž jej uhlopriečky a vyrobila tak dve trojuholníkové. Zisti, aká časť každej z nových šatiek je biela, aká šedá a aká čierna, ak v pôvodnej šatke bola čierna a šedá jej plochy.

Z6-II-3
Moje obľúbené čísla sú tie, ktoré sa po vynásobení svojim vlastným ciferným súčtom desaťkrát zväčšia. Súčin troch mojich obľúbených čísel je 71 668. Ktoré sú to čísla?

Z7-I-1
Janka plietla bratovi Lukášovi šál. Lukášovi sa šál vôbec nepáčil, a tak vždy večer potajomky z Jankiných v ten deň upletených riadkov štvrtinu vypáral. Janka začala pliesť v pondelok. V utorok uplietla o 24 radov viac ako v pondelok a v stredu dokonca dvakrát toľko ako v pondelok. Vo štvrtok uplietla už len 36 radov a hotový 180 – radový šál dala Lukášovi. Koľko radov uplietla Janka v utorok? Koľko radov vypáral Lukáš?

Z7-I-2
V štvorcovej sieti na obrázku sú znázornené všetky vrcholy dvoch štvorcov. Zisti obsah ich spoločnej časti.

Z7-I-3
Majo mal vynásobiť dve desatinné čísla. Desatinné čiarky si pomýlil s bodkami a vynásobil štyri celé čísla. Počítal bez chyby a vyšlo mu 15 228. Správny výsledok však mal byť 589,17. Aké čísla mal násobiť?

Z7-I-4
V tábore rozdeľovali vedúci deti do skupín po 5, posledná skupina však bola neúplná. Pri novej hre ich teda vedúci skúsili rozdeliť po 8 a opäť to „nevyšlo“. Pri druhej hre takto súťažilo o 4 skupiny menej ako pri prvej. V neúplných skupinách bol vždy párny počet detí. Koľko detí mohlo byť v tábore?

Z7-I-5
Označ vrcholy kocky celými číslami od 1 po 8 tak, aby pre každú jej stenu bol súčet príslušných čísel

    a) prvočíslo,
    b) iné prvočíslo.

Z7-I-6
Starý farmár sa rozhodol, že všetok svoj majetok – stádo oviec – rozdelí medzi svoje deti. Najprv rozdelil stádo na dve časti v pomere 1:3. Menšiu z nich dal prvorodenému, väčšiu opäť rozdelil v tom istom pomere. Z nových častí menšiu pridelil druhorodenému, väčšiu znovu rozdelil v pomere 1:3. Takto pokračoval, až kým každý z jeho synov nedostal svoj diel a zostávajúcu časť potom daroval svojej jedinej dcére. Zisti, koľko mal farmár oviec, ak vieš, že prostredný syn ich dostal 156. Ktoré z detí dostalo najviac oviec?

Z7-II-1
Bonboniéra s krabicou tvaru kvádra bola plná cukríkov, pekne uložených v riadkoch a stĺpcoch. Miško z nich niekoľko zjedol a tie, čo mu ostali, preusporiadal tak, že bez jedného miesta nimi zaplnil 3 celé riadky. Cukríky z neúplného riadku zjedol a zvyšné znovu preusporiadal. Tentoraz nimi zaplnil bez jedného miesta 5 celých stĺpcov. Nevyzeralo to pekne, preto cukríky z neúplného stĺpca zjedol a v bonboniére mu ostala už len tretina z pôvodného počtu cukríkov. Zisti

    a) koľko cukríkov bolo v plnej bonboniére,
    b) koľko cukríkov zjedol Miško predtým, ako ich prvýkrát preusporiadal.

Z7-II-2
Katka si z papiera vystrihla 20 obdĺžnikov. Prvý z nich mal rozmery 1 cm x 2 cm, druhý 2 cm x 3 cm, tretí 3 cm x 4 cm atď. Potom ich začala prikladať rovnako dlhými stranami k sebe tak, aby sa neprekrývali.

    a) Narysuj mnohouholník, ktorý Katka zložila z prvých šiestich svojich obdĺžnikov.
    b) Zisti obvod Katkinho mnohouholníka, zloženého zo všetkých vystrihnutých obdĺžnikov.

Z7-II-3
Pani učiteľka dala deťom na domácu úlohu vypočítať dva príklady na násobenie celých záporných čísel. Fero si ich oba napísal bez zátvoriek a doma si potom myslel, že sú to príklady na odčítanie (bodky si nevšimol). Takto zmenené príklady bezchybne vypočítal. Jeden z jeho výsledkov sa od toho „správneho“ líšil znamienkom, druhý zas bol -182 násobkom jeho prevrátenej hodnoty. Aké príklady Fero dostal na domácu úlohu?

Z8-I-1
Mišo si myslí trojciferné číslo. Jurovi prezradil, že ciferný súčet mysleného čísla je 8. Petrovi prezradil len ciferný súčin mysleného čísla. Peter správne určil, že takých čísel je 6 a povedal to Jurovi. Ten vyhlásil: „Už viem, aké sú cifry tvojho čísla, ale ešte mi to nestačí. Mišo obom chlapcom povedal:“ Druhá mocnina poslednej cifry nie je deliteľom mysleného čísla.“ To už chlapcom stačilo. Ktoré číslo si Mišo myslel?

Z8-I-2
Presne o polnoci z 31.12.2000 na 1.1.2001 mali v Plavákove slávnostne otvoriť nový, 160 cm hlboký bazén tvaru kvádra. Vodu do neho však začali napúšťať už 30.12. Graf na obrázku znázorňuje, ako sa menila výška vodnej hladiny v závislosti od času.

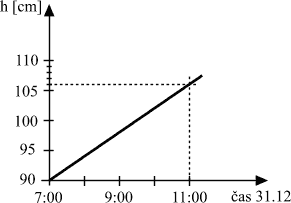
    a) Stihli včas napustiť bazén až po horný okraj?
    b) Kedy presne začali bazén napúšťať?

Z8-I-3
Starý farmár sa rozhodol, že všetok svoj majetok – stádo oviec – rozdelí medzi svoje deti. Najprv rozdelil stádo na dve časti v pomere 1:3. Menšiu z nich dal prvorodenému, väčšiu opäť rozdelil v tom istom pomere. Z nových častí menšiu pridelil druhorodenému, väčšiu znovu rozdelil v pomere 1:3. Takto pokračoval, až kým každý z jeho synov nedostal svoj diel a zostávajúcu časť potom daroval svojej jedinej dcére.
Zistite, koľko mal farmár synov, ak len jeden z nich dostal viac oviec, ako jeho dcéra.

Z8-I-4
Určite najväčší možný počet loptičiek, o priemere 100 mm, ktoré je možné uložiť do škatule tvaru kvádra o rozmeroch 100 cm x 100 cm x 10 cm.

Z8-I-5
Na nákladnom automobile sa pneumatiky na predných kolesách opotrebujú po 15 000 km, na zadných, zdvojených kolesách po 20 000 km. Šofér práve kúpil súpravu šiestich nových pneumatík. Koľko kilometrov maximálne môže na nich najazdiť?

Z8-I-6
Uhlopriečky delia kosoštvorec s obvodom 40 cm na 4 trojuholníky s celočíselnými dĺžkami strán. Aký najväčší obvod môže mať

    a) trojuholník
    b) štvoruholník
    c) päťuholník zložený z týchto trojuholníkov?

(Trojuholníky sa nesmú prekrývať a všetky 4 je treba použiť.)

Z8-II-1
Do spodného riadku tejto čudnej sčítacej pyramídy doplňte čísla 1, 1, 2, 2, 3, 3 a 4 tak, aby hore vyšlo čo najväčšie číslo.

Z8-II-2
V pravidelnom šesťuholníku s obsahom 144 cm² sme vyznačili všetky uhlopriečky. Šesťuholník sa nám takto „rozpadol“ na niekoľko trojuholníkov a štvoruholníkov.

    a) Zistite, na koľko častí ho uhlopriečky rozdelili.
    b) Určte obsah pravidelného šesťuholníka, ktorý vznikne zložením všetkých štvoruholníkových častí daného šesťuholníka.

Z8-II-3
Pri ohni sedeli náčelníci troch spriatelených indiánskych kmeňov s tromi rovnakými fajkami. Mali bojovú poradu a fajčili. Prvý z nich vyfajčí celú fajku za desať minút, druhý za pol hodiny a tretí za hodinu. V okamihu, keď niektorý z nich bude mať prázdnu fajku, musia bojovú poradu ukončiť. Ako si majú náčelníci medzi sebou vymieňať fajky, aby sa mohli radiť čo najdlhšie? Ako dlho by v takomto prípade trvala ich bojová porada?

Z9-I-1
Štvoruholník, ktorý nemá žiadne dve strany rovnako dlhé, budeme volať nerovnakostranný. Pravidelný 12-uholník má obsah 81 cm². Narysujte všetky také tvarovo rôzne nerovnakostranné štvoruholníky s vrcholmi vo vrcholoch tohto 12-uholníka a zistite obsah každého z nich.

Z9-I-2
V hokejovom turnaji Zelení 3 krát vyhrali a umiestnili sa na 1. mieste s celkovým skóre 7:1. Červení dosiahli skóre 2:3 a Modrí 3:3. Poslední Hnedí prehrali všetky tri zápasy a ich celkové skóre bolo 1:6. Vyplňte tabuľku zápasov, ak ešte viete, že Zelení porazili Červených 3:0 a že Červení i Modrí práve raz vyhrali, raz prehrali a raz remizovali.

	Zelení	Červení	Modrí	Hnedí	Skóre
Zelení	X
Červení		X
Modrí			X
Hnedí				X

Z9-I-3
Osovo súmerný päťuholník s obsahom 27 cm² má práve tri vnútorné uhly pravé a práve 3 strany zhodné. Zistite veľkosti ďalších dvoch vnútorných uhlov päťuholníka a dĺžku niektorej z trojice zhodných strán.

Z9-I-4
Moja mama sa narodila 16.3. 1948. Je to pekný dátum, platí totiž 16 × 3 = 48. V ktorých rokoch 20. storočia bolo najviac takýchto pekných dátumov?

Z9-I-5
Ku každej stene kocky s hranou dĺžky a sme prilepili taký pravidelný 4-boký ihlan, že vzniklo teleso s 12 stenami. Koľko má toto teleso vrcholov? O koľko % má zlepené teleso väčší objem ako pôvodná kocka?

Z9-I-6
Ostrov obrov má rovnako veľa obyvateľov ako Ostrov trpaslíkov. Ani na jednom z týchto ostrovov nežijú dve rovnako ťažké bytosti a okrem dvoch obrov a dvoch trpaslíkov má každý na svojom ostrove dvoch kamarátov, z ktorých je jeden o 2 kg od neho ťažší a druhý o 2 kg od neho ľahší. Dvaja najťažší trpaslíci vážia spolu toľko, čo najľahší obor, traja „prostrední“ trpaslíci vážia spolu toľko, čo prostredný obor a štyria najľahší trpaslíci toľko, čo ôsmy najťažší obor. Zistite, koľko obyvateľov má Ostrov trpaslíkov a o koľko kg je najťažší obor ťažší, ako najľahší trpaslík.

Z9-II-1
Milka si myslela dvojciferné číslo. Zmenila poradie cifier a dostala číslo, ktoré sa od pôvodného líšilo o 75%. Aké číslo si mohla myslieť?

Z9-II-2
Andrea triedi trojuholníky, ktorých strany vyjadrené v cm sú celé čísla, na úzke, široké a ostatné. Úzky trojuholník je taký, v ktorom je súčet dĺžok niektorých dvoch strán len o 1 cm väčší, ako dĺžka tretej strany. Široký trojuholník je taký, v ktorom je súčet dĺžok niektorých dvoch strán dvojnásobkom dĺžky tretej strany. Nájdite

    a) všetky úzke trojuholníky, ktorých dve strany merajú 6 cm a 8 cm,
    b) všetky široké trojuholníky, ktorých dve strany merajú 4 cm a 3 cm,
    c) všetky trojuholníky, ktorých jedna strana meria 5 cm a sú široké aj úzke súčasne.

Z9-II-3
Dvaja cyklisti vyšli súčasne z toho istého miesta na výlet. Prešli tú istú trasu a vrátili sa naraz domov. Cestou obaja odpočívali. Prvý išiel dvakrát tak dlho, ako druhý odpočíval. Druhý išiel štyrikrát tak dlho, ako odpočíval prvý. Kto z nich jazdí na bicykli rýchlejšie a koľkokrát?

Z9-II-4
V Squarlande žijú iba štvorce. Až na dve výnimky tam každý z nich má priateľa, ktorý má od neho o 8 cm väčší obvod a priateľa s obvodom o 8 cm menším. Priemerná dĺžka strany squarlandského štvorca je 15 cm. Žiadne dva z nich nie sú zhodné a obvod najmenšieho je rovný dĺžke strany najväčšieho. Zistite

    a) počet obyvateľov Squarlandu,
    b) rozmery najmenšieho a rozmery najväčšieho squarlandského štvorca,
    c) priemerný obsah „Squarlanďana“.

Z9-III-1
Skupinka detí si zorganizovala piškvorkový turnaj. Každý hral s každým a celkom odohrali 136 zápasov. Z toho práve 66 zápasov bolo typu dievča – dievča alebo chlapec – chlapec. Koľko bolo v skupinke chlapcov a koľko dievčat?

Z9-III-2
V Squarlande žijú iba štvorce. Až na dve výnimky tam každý z nich má priateľa, ktorý má od neho o 8 cm väčší obvod a priateľa s obvodom o 8 cm menším. Priemerný obsah squarlandského štvorca je 116 cm². Žiadne dva z nich nie sú zhodné a obvod najmenšieho je rovný dĺžke strany najväčšieho. Zistite

    a) počet obyvateľov Squarlandu,
    b) rozmery najmenšieho a rozmery najväčšieho squarlandského štvorca,
    c) priemernú dĺžku strany „Squarlanďana“.

Z9-III-3
Na svojich potulkách objavil profesor Hmyzuli nový druh chrobáka. Podľa počtu jeho nožičiek a tvaru jednotlivých článkov ho nazval Guľôčkovcom Dvanásťnôžkovým: každý článok tohto chrobáka má tvar gule a z každého článku okrem prvého (hlavičky) vyrastajú dva páry nožičiek. Navyše, každý z článkov má o 21% väčší prierez, ako článok za ním. Zistite presnú dĺžku chrobáka, ak viete, že hlavička má polomer 0,2662 cm.

Z9-III-4
Marta triedi trojuholníky, ktorých strany vyjadrené v cm sú celé čísla, na vysoké, nízke a ostatné. Vysoký trojuholník je taký, v ktorom sa súčet dĺžok niektorých dvoch strán rovná štvornásobku dĺžky tretej strany. Nízky trojuholník je taký, v ktorom je súčin dĺžok niektorých dvoch strán dvojnásobkom dĺžky tretej strany. Nájdite

    a) všetky vysoké trojuholníky, ktorých jedna strana meria 6 cm,
    b) všetky nízke trojuholníky, ktorých jedna strana meria 6 cm,
    c) všetky trojuholníky, ktorých jedna strana meria 4 cm a sú vysoké a nízke súčasne.

Uložiť

Uložiť