58. ročník matematickej olympiády 2008-2009

C	B	A
domáce kolo	domáce kolo	domáce kolo
školské kolo	školské kolo	školské kolo
krajské kolo	krajské kolo	krajské kolo
		celoštátne kolo

C-I-1
Tomáš, Jakub, Martin a Peter organizovali na námestí zbierku pre dobročinné účely. Za chvíľu sa pri nich postupne zastavilo päť okoloidúcich. Prvý dal Tomášovi do jeho pokladničky 3 Sk, Jakubovi 2 Sk, Martinovi 1 Sk a Petrovi nič. Druhý dal jednému z chlapcov 8 Sk a ostatným trom nedal nič. Tretí dal dvom chlapcom po 2 Sk a dvom nič. Štvrtý dal dvom chlapcom po 4 Sk a dvom nič. Piaty dal dvom chlapcom po 8 Sk a dvom nič. Potom chlapci zistili, že každý z nich vyzbieral inú čiastku, pričom tieto tvoria štyri po sebe idúce prirodzené čísla. Ktorý z chlapcov vyzbieral najmenej a ktorý najviac korún?

C-I-2
Pravouhlému trojuholníku ABC s preponou AB je opísaná kružnica. Päty kolmíc z bodov A, B na dotyčnicu k tejto kružnici v bode C označme D, E. Vyjadrite dĺžku úsečky DE pomocou dĺžok odvesien trojuholníka ABC.

C-I-3
Nájdite všetky štvorciferné čísla n, ktoré majú nasledujúce tri vlastnosti: V zápise čísla n sú dve rôzne cifry, každá dvakrát. Číslo n je deliteľné siedmimi. Číslo, ktoré vznikne otočením poradia ci?er čísla n, je tiež štvorciferné a deliteľné siedmimi.

C-I-4
Daný je konvexný päťuholník ABCDE. Na polpriamke BC zostrojte taký bod G, aby obsah trojuholníka ABG bol zhodný s obsahom daného päťuholníka.

C-I-5
Z množiny {1, 2, 3, …, 99} vyberte čo najväčší počet čísel tak, aby súčet žiadnych dvoch vybraných čísel nebol násobkom jedenástich. (Vysvetlite, prečo zvolený výber má požadovanú vlastnosť a prečo žiadny výber väčšieho počtu čísel nevyhovuje.)

C-I-6
Dokážte, že pre ľubovoľné rôzne kladné čísla a, b platí

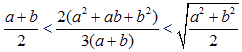▲ hore ▲

C-S-1
Dokážte, že pre ľubovoľné nezáporné čísla a, b, c platí

(a + bc)(b + ac) ≥ ab(c + 1)²

Zistite, kedy nastane rovnosť.

C-S-2
V pravouhlom trojuholníku ABC označíme P pätu výšky z vrcholu C na preponu AB. Priesečník úsečky AB s priamkou, ktorá prechádza vrcholom C a stredom kružnice vpísanej trojuholníku PBC, označíme D. Dokážte, že úsečky AD a AC sú zhodné.

C-S-3
Keď isté dve prirodzené čísla v rovnakom poradí sčítame, odčítame, vydelíme a vynásobíme a všetky štyri výsledky sčítame, dostaneme 2 009. Určte tieto dve čísla.

▲ hore ▲

C-II-1
Uvažujme výraz

    a)   Dokážte, že pre každé reálne číslo x platí V(x) ≥ 3.
    b)   Nájdite najväčšiu hodnotu V(x).

C-II-2
V pravouhlom trojuholníku ABC označíme P pätu výšky z vrcholu C na preponu AB a D, E stredy kružníc vpísaných postupne trojuholníkom APC, CPB. Dokážte, že stred kružnice vpísanej trojuholníku ABC je priesečníkom výšok trojuholníka CDE.

C-II-3
Z množiny {1, 2, 3, …, 99} je vybraných niekoľko rôznych čísel tak, že súčet žiadnych troch z nich nie je násobkom deviatich.

    a)   Dokážte, že medzi vybranými číslami sú najviac štyri deliteľné tromi.
    b)   Ukážte, že vybraných čísel môže byť 26.

C-II-4
Pravouhlému trojuholníku ABC s preponou AB a obsahom S je opísaná kružnica. Dotyčnica k tejto kružnici v bode C pretína dotyčnice vedené bodmi A a B v bodoch D a E. Vyjadrite dĺžku úsečky DE pomocou dĺžky c prepony a obsahu S.

▲ hore ▲

B-I-1
Na tabuli je napísané štvorciferné číslo deliteľné ôsmimi, ktorého posledná cifra je 8. Keby sme poslednú cifru nahradili cifrou 7, získali by sme číslo deliteľné deviatimi. Keby sme však poslednú cifru nahradili cifrou 9, získali by sme číslo deliteľné siedmimi. Určte číslo, ktoré je napísané na tabuli.

B-I-2
Určte všetky trojice (x, y, z) reálnych čísel, pre ktoré platí

x² + xy = y² + z²,
z² + zy = y² + x².

B-I-3
Na strane BC, resp. CD rovnobežníka ABCD určte body E, resp. F tak, aby úsečky EF, BD boli rovnobežné a trojuholníky ABE, AEF a AFD mali rovnaké obsahy.

B-I-4
Na pláne 7×7 hráme hru lode. Nachádza sa na nej jedna loď 2×3. Môžeme sa spýtať na ľubovoľné políčko plánu, a ak loď zasiahneme, hra končí. Ak nie, pýtame sa znova. Určte najmenší počet otázok, ktoré potrebujeme, aby sme s istotou loď zasiahli.

B-I-5
Trojuholníku ABC je opísaná kružnica k. Os strany AB pretne kružnicu k v bode K, ktorý leží v polrovine opačnej k polrovine ABC. Osi strán AC a BC pretnú priamku CK postupne v bodoch P a Q. Dokážte, že trojuholníky AKP a KBQ sú zhodné.

B-I-6
Nájdite všetky dvojice celých čísel (m, n), pre ktoré je hodnota výrazu

celé kladné číslo.

▲ hore ▲

B-S-1
V obore reálnych čísel riešte sústavu rovníc

ax + y = 2,
x – y = 2a,
x + y = 1

s neznámymi x, y a reálnym parametrom a.

B-S-2
Pre vnútorný bod P strany AB ostrouhlého trojuholníka ABC označme K a L päty kolmíc z bodu P na priamky AC a BC. Zostrojte taký bod P, pre ktorý priamka CP rozpoľuje úsečku KL.

B-S-3
Číslo nazveme „magickým“ práve vtedy, keď sa dá vyjadriť ako súčet trojciferného čísla m a trojciferného čísla m´ zapísaného rovnakými číslicami v opačnom poradí. Niektoré „magické“ čísla možno takto vyjadriť viacerými spôsobmi; napríklad 1554 = 579 + 975 = 777 + 777. Určte všetky „magické“ čísla, ktoré majú takých vyjadrení m + m´ čo najviac. (Na poradie m a m´ neberieme ohľad.)

▲ hore ▲

B-II-1
V obore reálnych čísel riešte sústavu rovníc

x + y = 1,
x – y = a,
-4ax + 4y = z² + 4

s neznámymi x, y, z a reálnym parametrom a.

B-II-2
Na pláne 5×5 hráme hru lode. Zo štyroch políčok plánu je vytvorená jedna loď niektorého z tvarov na obrázku. Môžeme sa spýtať na ľubovoľné políčko plánu, a ak loď zasiahneme, hra končí.

    a)   Navrhnite osem políčok, na ktoré sa stačí spýtať, aby sme mali istotu zásahu lode.
    b)   Zdôvodnite, prečo žiadnych sedem otázok takú istotu nedáva.

B-II-3
Je daný ostrouhlý trojuholník ABC, ktorý nie je rovnoramenný. Označme K priesečník osi uhla ACB s osou strany AB. Priamka CK pretína výšky z vrcholov A a B v bodoch, ktoré označíme postupne P a Q. Predpokladajme, že trojuholníky AKP a BKQ majú rovnaký obsah. Určte veľkosť uhla ACB.

B-II-4
K ľubovoľnému prirodzenému číslu určíme jeho zvyšky po delení každým z desiatich prirodzených čísel 2, 3, 4, …, 11 a týchto desať zvyškov (niektoré môžu byť nulové) sčítame. Určte všetky také eísla menšie ako 25 000, ktoré majú uvedený súčet čo najmenší. (Nulu za prirodzené číslo nepovažujeme).

▲ hore ▲

A-I-1
V obore reálnych čísel riešte sústavu rovníc

2sinx.cos(x + y) + siny = 1,
2siny.cos(y + x) + sinx = 1.

A-I-2
Daný je tetivový štvoruholník ABCD. Dokážte, že spojnica priesečníkov výšok trojuholníka ABC s priesečníkom výšok trojuholníka ABD je rovnobežná s priamkou CD.

A-I-3
Nájdite všetky dvojice prirodzených čísel x, y také, že    je prvočíslo.

A-I-4
Uvažujme nekonečnú aritmetickú postupnosť

a, a + d, a + 2d, …,      (*)

kde a, d sú prirodzené (t. j. kladné celé) čísla.

    a)   Nájdite príklad postupnosti (*), ktorá obsahuje nekonečne veľa k-tych mocnín prirodzených čísel pre všetky k = 2, 3, …
    b)   Nájdite príklad postupnosti (*), ktorá neobsahuje žiadnu k-tu mocninu prirodzeného čísla pre žiadne k = 2, 3, …
    c)   Nájdite príklad postupnosti (*), ktorá neobsahuje žiadnu druhú mocninu prirodzeného čísla, ale obsahuje nekonečne veľa tretích mocnín prirodzených čísel.
    d)   Dokážte, že pre všetky prirodzené čísla a, d, k (k < 1) platí: Postupnosť (*) buď neobsahuje žiadnu k-tu mocninu prirodzeného čísla, alebo obsahuje nekonečne veľa k-tych mocnín prirodzených čísel.

A-I-5
V každom vrchole pravidelného 2008-uholníka leží jedna minca. Vyberieme dve mince a premiestnime každú z nich do susedného vrcholu tak, že jedna sa posunie v smere a druhá proti smeru chodu hodinových ručičiek. Rozhodnite, či je možné týmto spôsobom všetky mince postupne presunúť:

    a)   na 8 kôpok po 251 minciach,
    b)   na 251 kôpok po 8 minciach.

A-I-6
Daný je trojuholník ABC. Vnútri strán AC, BC sú dané body E, D tak, že |AE| = |BD|. Označme M stred strany AB a P priesečník priamok AD a BE. Dokážte, že obraz bodu P v stredovej súmernosti so stredom M leží na osi uhla ACB.

▲ hore ▲

A-S-1
Zistite, pre ktoré dvojice kladných celých čísel m a n platí .

A-S-2
Nech ABC je ostrouhlý trojuholník, v ktorom vnútorný uhol pri vrchole A má veľkosť 45°. Označme D pätu výšky z vrcholu C. Uvažujme ďalej ľubovoľný vnútorný bod P výšky CD. Dokážte tvrdenie: Priamky AP a BC sú navzájom kolmé práve vtedy, keď úsečky AP a BC sú zhodné.

A-S-3
Určte všetky prirodzené čísla, ktorými možno krátiť niektorý zo zlomkov tvaru , kde p a q sú nesúdeliteľné celé čísla.

▲ hore ▲

A-II-1
Isté štvorciferné prirodzené číslo je deliteľné siedmimi. Ak zapíšeme jeho číslice v opačnom poradí, dostaneme väčšie štvorciferné číslo, ktoré je tieľ deliteľné siedmimi. Navyše po delení číslom 37 dávajú obe spomenuté štvorciferné čísla rovnaký zvyšok. Určte pôvodné štvorciferné číslo.

A-II-2
Na odvesnách dĺžok a, b pravouhlého trojuholníka ležia postupne stredy dvoch kružníc k_a, k_b. Obe kružnice sa dotýkajú prepony a prechádzajú vrcholom oproti prepone. Polomery uvedených kružníc označme r_a, r_b. Určte najväčšie kladné reálne číslo p také, že nerovnosť

platí pre všetky pravouhlé trojuholníky.

A-II-3
Určte veľkosti vnútorných uhlov a, b, g trojuholníka, pre ktoré platí

2sin b . sin(a + b) – cos a = 1;
2sin g . sin(b + g) – cos b = 0.

▲ hore ▲