59. ročník matematickej olympiády 2009-2010

C	B	A
domáce kolo	domáce kolo	domáce kolo
školské kolo	školské kolo	školské kolo
krajské kolo	krajské kolo	krajské kolo
		celoštátne kolo

C-I-1
Erika a Klárka hrali hru „slovný logik“ s týmito pravidlami: Hráč A si myslí slovo zložené z piatich rôznych písmen. Hráč B vysloví ľubovoľné slovo zložené z piatich rôznych písmen a hráč A mu prezradí,
koľko písmen uhádol na správnej pozícii a koľko na nesprávnej. Písmená považujeme za rôzne, aj keď sa líšia len dĺžňom alebo mäkčeňom (napríklad písmená A, Á sú rôzne). Keby si napríklad hráč A myslel
slovo LOĎKA a B by vyslovil slovo KOLÁČ, odpovedal by mu hráč A, že uhádol jedno písmeno na správnej pozícii a dve na nesprávnej. Skrátene by povedal „1 + 2“, lebo obe slová sa naozaj zhodujú len
v písmene O vrátane pozície (druhé písmeno zľava) a v písmenách K a L, ktorých pozície sú odlišné.
Erika si myslela slovo zložené z piatich rôznych písmen a Klárka vyslovila slová KABÁT, STRUK, SKOBA, CESTA a ZÁPAL. Erika na tieto slová v danom poradí odpovedala 0+3, 0+2, 1+2, 2+0 a 1+2. Zistite, ktoré slovo si Erika mohla myslieť.

C-I-2
Vrcholom C pravouholníka ABCD veďte priamky p a q, ktoré majú s daným pravouholníkom spoločný iba bod C, pričom priamka p má od bodu A najväčšiu možnú vzdialenosť a priamka q vymedzuje s priamkami AB a AD trojuholník s čo najmenším obsahom.

C-I-3
Určte všetky reálne čísla x, ktoré vyhovujú rovnici 4x – 2 = 5. (Symbol označuje najväčšie celé číslo, ktoré nie je väčšie ako číslo x, tzv. dolnú celú časť reálneho čísla x.)

C-I-4
Kružnica k(S; r) sa dotýka priamky AB v bode A. Kružnica l(T; s) sa dotýka priamky AB v bode B a pretína kružnicu k v krajných bodoch C, D jej priemeru. Vyjadrite dĺžku a úsečky AB pomocou polomerov r, s. Dokážte ďalej, že priesečník M priamok CD, AB je stredom úsečky AB.

C-I-5
Dokážte, že pre ľubovoľné kladné reálne čísla a, b platí

a pre každú z oboch nerovností zistite, kedy prechádza v rovnosť.

C-I-6
Nájdite všetky prirodzené čísla, ktoré nie sú deliteľné desiatimi a ktoré majú vo svojom dekadickom zápise niekde vedľa seba dve nuly, po ktorých vyškrtnutí sa pôvodné číslo 89-krát zmenší.

▲ hore ▲

C-S-1
Ak zväčšíme čitateľ aj menovateľ istého zlomku o 1, dostaneme zlomok o hodnotu 1/20 väčší. Ak urobíme s väčším zlomkom rovnakú operáciu, dostaneme zlomok o hodnotu 1/12 väčší, ako bola hodnota zlomku na začiatku. Určte všetky tri zlomky.

C-S-2
Kružnice k(S; 6 cm) a l(O; 4 cm) majú vnútorný dotyk v bode B. Určte dĺžky strán trojuholníka ABC, pričom bod A je priesečník priamky OB s kružnicou k a bod C je priesečník kružnice k s dotyčnicou z bodu A ku kružnici l.

C-S-3
Nájdite všetky dvojice nezáporných celých čísel a, b, pre ktoré platí

a² + b + 2 = a + b².

▲ hore ▲

C-II-1
Dokážte, že pre ľubovoľné celé čísla n a k väčšie ako 1 je číslo n^k + 2 – n^k deliteľné
dvanástimi.

C-II-2
Dokážte, že pre ľubovoľné čísla a, b z intervalu <1, ∞) platí nerovnosť

(a² + 1)(b² + 1) – (a – 1)²(b – 1)² ≥ 4

a zistite, kedy nastane rovnosť.

C-II-3
Daná je kružnica k so stredom S. Kružnica l má väčší polomer ako kružnica k, prechádza jej stredom a pretína ju v bodoch M a N. Priamka, ktorá prechádza bodom N a je rovnobežná s priamkou MS, vytína na kružniciach tetivy NP a NQ. Dokážte, že trojuholník MPQ je rovnoramenný.

C-II-4
Určte všetky dvojice reálnych čísel x, y, ktoré vyhovujú sústave rovníc

ak    a)  p = 2,
       b)  p = 3.

Symbol označuje najväčšie celé číslo, ktoré nie je väčšie ako dané reálne číslo x (tzv. dolná celá časť reálneho čísla x).

▲ hore ▲

B-I-1
Na stole sú tri kôpky zápaliek: v jednej 2 009, v druhej 2 010, v tretej 2 011. Hráč, ktorý je na ťahu, zvolí dve kôpky a z každej z nich odoberie po jednej zápalke. V hre sa pravidelne striedajú dvaja hráči. Hra končí, akonáhle niektorá kôpka zmizne. Vyhráva ten hráč, ktorý urobil posledný ťah. Opíšte stratégiu jedného z hráčov, ktorá mu zaručí výhru.

B-I-2
Na tabuli je napísané štvorciferné číslo, ktoré má presne šesť kladných deliteľov, z ktorých práve dva sú jednociferné a práve dva dvojciferné. Väčší z dvojciferných deliteľov je druhou mocninou prirodzeného čísla. Určte všetky čísla, ktoré môžu byť na tabuli napísané.

B-I-3
V rovine je daná úsečka AB. Zostrojte rovnobežník ABCD, pre ktorého stredy strán AB, CD, DA označené postupne K, L, M platí: body A, B, L, D ležia na jednej kružnici a aj body K, L, D, M ležia na jednej kružnici.

B-I-4
Nájdite 2 009 po sebe idúcich štvorciferných čísel, ktorých súčet je súčinom troch po sebe idúcich prirodzených čísel.

B-I-5
Vnútri kratšieho oblúka AB kružnice opísanej rovnostrannému trojuholníku ABC zvolíme bod D. Tetiva CD pretína stranu AB v bode E. Dokážte, že trojuholník so stranami dĺžok |AE|, |BE|, |CE| je podobný trojuholníku ABD.

B-I-6
Reálne čísla a, b majú túto vlastnosť: rovnica x² – ax + b – 1 = 0 má v množine reálnych čísel dva rôzne korene, ktorých rozdiel je kladným koreňom rovnice x² – ax + b + 1 = 0.

    a)   Dokážte nerovnosť b > 3,
    b)   Pomocou b vyjadrite korene oboch rovníc.

▲ hore ▲

B-S-1
Určte všetky hodnoty reálnych parametrov p, q, pre ktoré má každá z rovníc

x(x – p) = 3 + q,   x(x + p) = 3 – q

v obore reálnych čísel dva rôzne korene, ktorých aritmetický priemer je jedným z koreňov zvyšnej rovnice.

B-S-2
Dané sú dĺžky odvesien a=|BC|, b=|AC| pravouhlého trojuholníka ABC, pričom a>b. Označme D stred prepony AB a E (E≠C) priesečník strany BC s kružnicou opísanou trojuholníku ADC. Vypočítajte obsah trojuholníka EAD.

B-S-3
Určte všetky dvojice celých kladných čísel m, n, pre ktoré platí 37 + 27^m = n³.

▲ hore ▲

B-II-1
Kružnica l(T;s) prechádza stredom kružnice k(S;2cm). Kružnica m(U;t) sa zvonka dotýka kružníc k a l, pričom US ^ ST. Polomery s a t vyjadrené v centimetroch sú celé čísla. Určte ich.

B-II-2
V matematickej súťaži bolo zadaných 7 úloh a za každú z nich mohol súťažiaci získať 0, 1 alebo 2 body. Súťaže sa zúčastnilo 60 žiakov. Za každú úlohu bolo udelených aspoň 95 bodov. Dokážte, že medzi súťažiacimi nájdeme dvoch takých, že každú z úloh vyriešil aspoň jeden z nich za 2 body.

B-II-3
V rovine je daný rovnobežník ABCD. Označme postupne K, L, M stredy strán AB, CD, AD. Predpokladajme, že body A, B, L, D ležia na jednej kružnici a súčasne aj body K, L, D, M ležia na jednej kružnici. Dokážte, že |AC| = 2·|AD|.

B-II-4
Číslo n je súčinom štyroch prvočísel. Ak každé z týchto prvočísel zväčšíme o 1 a vzniknuté štyri čísla vynásobíme, dostaneme číslo o 2886 väčšie ako pôvodné číslo n. Určte všetky také n.

▲ hore ▲

A-I-1
V obore reálnych čísel riešte sústavu rovníc

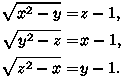
A-I-2
Do kosoštvorca ABCD je vpísaná kružnica. Uvažujme jej ľubovoľnú dotyčnicu pretínajúcu obe strany BC, CD a označme postupne R, S jej priesečníky s priamkami AB, AD. Dokážte, že hodnota súčinu |BR|.|DS| od voľby dotyčnice nezávisí.

A-I-3
Na tabuli sú napísané čísla 1, 2, …, 33. V jednom kroku zvolíme na tabuli dve čísla, z ktorých jedno je deliteľom druhého, obe zotrieme a na tabuľu napíšeme ich (celočíselný) podiel. Takto pokračujeme, kým na tabuli nezostanú iba čísla, z ktorých žiadne nie je deliteľom iného. (V jednom kroku môžeme zotrieť aj dve rovnaké čísla a nahradiť ich číslom 1.) Koľko najmenej čísel môže na tabuli zostať?

A-I-4
V ľubovoľnom ostrouhlom rôznostrannom trojuholníku ABC označme O, V a S postupne stred kružnice opísanej, priesečník výšok a stred kružnice vpísanej. Dokážte, že os úsečky OV prechádza bodom S práve vtedy, keď jeden vnútorný uhol trojuholníka ABC má veľkosť 60°.

A-I-5
V nádrži je r₀ rýb, spoločný úlovok n rybárov. Prichádzajú pre svoj podiel jednotlivo. Každý si myslí, že sa dostavil ako prvý, a aby si vzal presne n-tinu aktuálneho počtu rýb v nádrži, musí predtým jednu z rýb pustiť späť do mora. Určte najmenšie možné číslo r₀ v závislosti od daného n ≥ 2, keď aj posledný rybár si aspoň jednu rybu odnesie.

A-I-6
Pre dané prvočíslo p určte počet (všetkých) usporiadaných trojíc (a, b, c) čísel z množiny {1, 2, 3, …, 2p²}, ktoré spĺňajú vzťah

pričom [x, y] označuje najmenší spoločný násobok čísel x a y.

▲ hore ▲

A-S-1
V obore reálnych čísel riešte sústavu rovníc

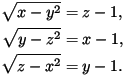
A-S-2
Nájdite všetky možné hodnoty podielu

pričom r je polomer kružnice opísanej a ρ polomer kružnice vpísanej pravouhlému trojuholníku s odvesnami dĺžok a a b.

A-S-3
Na tabuli sú napísané čísla 1, 2, …, 33. V jednom kroku zvolíme niekoľko čísel napísaných na tabuli (aspoň dve), ktorých súčin je druhou mocninou prirodzeného čísla, zvolené čísla zotrieme a na tabuľu napíšeme druhú odmocninu z ich súčinu. Takto pokračujeme, až na tabuli ostanú iba také čísla, že súčin žiadnych z nich nie je druhou mocninou. Koľko najmenej čísel môže na tabuli ostať?

▲ hore ▲

A-II-1
Dokážte, že rovnica x² + p|x| = qx – 1 s reálnymi parametrami p, q má v obore reálnych čísel štyri riešenia práve vtedy, keď platí p + |q| + 2 < 0.

A-II-2
Daný je rovnobežník ABCD s tupým uhlom ABC. Na jeho uhlopriečke AC v polrovine BDC zvoľme bod P tak, aby platilo |BPD| = |ABC|. Dokážte, že priamka CD je dotyčnicou ku kružnici opísanej trojuholníku BCP práve vtedy, keď úsečky AB a BD sú zhodné.

A-II-3
Určte všetky celé kladné čísla m, n také, že n delí 2m – 1 a m delí 2n – 1.

A-II-4
V ľubovoľnom trojuholníku ABC označme O stred kružnice vpísanej, P stred kružnice pripísanej ku strane BC a D priesečník osi uhla CAB so stranou BC. Dokážte, že platí

(Kružnica pripísaná ku strane BC je taká kružnica, ktorá sa dotýka jednak strany BC, jednak oboch polpriamok opačných k polpriamkam BA a CA.)

▲ hore ▲