75. ročník matematickej olympiády 2025-2026
Súťažné úlohy kategórií Z5-Z9

aktualizované 05.01.2026 14:30

Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce
okresné	okresné	okresné	okresné	okresné
				krajské

Z5-I-1
Zvláštna kalkulačka má iba dve funkčné tlačidlá. Po stlačení prvého tlačidla sa k číslu na displeji pripočíta číslo 1, po stlačení druhého tlačidla sa číslo na displeji vynásobí číslom 2. Na displeji po každom stlačení tlačidla svieti správny výsledok.
Nájdite dva rôzne spôsoby, ako pomocou 6 stlačení tlačidiel dostať na displeji z čísla 1 číslo 15.

Z5-I-2
K zámku patrí park v tvare štvorca so stranou dĺžky 240 metrov. Náčrt parku je na obrázku. Po stranách štvorca vedú cesty, v jeho vrcholoch stoja agát, buk, céder a dub. Park križujú dva ďalšie chodníky rovnobežné so strana mi štvorcového parku – jeden vedie od javora k studničke, druhý vedie od lipy k orechu.

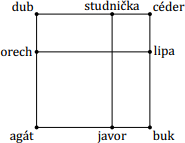
Princezná pri svojich prechádzkach parkom chodila len po cestách a chodníkoch, nikdy sa nevracala, ani zbytočne neodbočovala. Zistila, že:
• prechádzka od buka k studničke okolo javora, agáta, orecha a duba je dvakrát dlhšia ako okolo lipy a cédra,
• prechádzka od buka k studničke okolo lipy a cédra je rovnako dlhá ako prechádzka od duba k lipe okolo studničky a cédra.
Aká dlhá je priama cesta od agáta k orechu?

Z5-I-3
Danka a Janka každá pre seba nazbierali jahody. Keby mala Janka o polovicu viac jahôd, než nazbierala, mala by ich rovnako ako Danka. Keby mala Janka dvakrát viac jahôd, než nazbierala, mala by ich o 48 viac ako Danka.
Koľko jahôd nazbierala Janka a koľko Danka?

Z5-I-4
Anežka správne vynásobila určité prirodzené číslo číslom 7 a výsledné päťciferné číslo napísala na papier. Papagáj kus papiera vyďobal, a tak sa prvá cifra výsledku stala nečitateľnou. Na zvyšku papiera zostalo napísané 2887.
Aká mohla byť prvá cifra Anežkinho výsledku? Nájdite všetky možnosti.

Z5-I-5
Veky siedmich kamarátov sú 8, 9, 10, 11, 11, 13 a 14 rokov. Traja kamaráti sú práve v kine, dvaja sú na futbale a dvaja doma. Súčet vekov tých v kine je 30 rokov a súčet vekov tých na futbale je 24 rokov. Každý z kamarátov na futbale má viac rokov ako Ondrej, ktorý zostal doma.
Koľko rokov môže mať Ondrej? Nájdite všetky možnosti.

Z5-I-6
Štyri dievčatá dláždili štvorcovými dlaždicami terasu v rohu dvora. Viola používala dlaždice so stranou 1 dm, Ruženka so stranou 2 dm, Bianka so stranou 3 dm a Karmen so stranou 4 dm. Prvé z dievčat položilo jednu zo svojich dlaždíc do rohu. Druhé položilo svoje dlaždice pozdĺž voľných strán predchádzajúcej dlaždice a pridalo jednu navyše tak, aby vznikol štvorec (napríklad ako na obrázku).

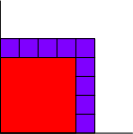
Podobným spôsobom položilo svoje dlaždice tretie a nakoniec aj štvrté dievča. Takto pokryli štvorcovú terasu bez medzier a prekryvov.
V akom poradí mohli dievčatá klásť dlaždice a koľko dlaždíc celkovo použili? Nájdite všetky možnosti.

Z5-II-1

Z5-II-2

Z5-II-3

Z6-I-1
V nasledujúcom sčítacom algebrograme zodpovedajú rôzne písmená rôznym cifrám a rovnaké rovnakým:

T	O	N	A
	O	N	A
		N	A
			A
8	6	5	4

Z6-I-2
Od 1. januára bol pán Novák zamestnaný v novej firme, pričom nástupná výška jeho platu bola 1 550 eur mesačne.
Pretože sa osvedčil, od istého mesiaca v prvom polroku mu zvýšili plat o niekoľko celých eur. Takýto plat dostával mesačne už vo všetkých ďalších mesiacoch. Za celý rok si zarobil dokopy 20 000 eur.
Za ktorý mesiac mohol dostať prvýkrát zvýšený plat a o koľko eur? Nájdite všetky možnosti.

Z6-I-3
Obdĺžnik ABCD rozmerov 8 × 6 je pomocou vodorovných a zvislých čiar rozdelený na rovnaké štvorčeky a bod N leží v štvrtine jeho dlhšej strany AB bližšie k A, tak ako vidíme na obrázku.

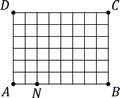
Rozdeľte obdĺžnik ABCD tromi úsečkami so spoločným bodom N na štyri časti s rovnakými obsahmi.

Z6-I-4
Majme jedno trojciferné a jedno dvojciferné číslo. Trojciferné číslo zaokrúhlime na stovky a dvojciferné zaokrúhlime na desiatky. Rozdiel zaokrúhlených čísel je 500.
Aký najmenší a aký najväčší môže byť rozdiel pôvodných nezaokrúhlených čísel?

Z6-I-5
Peťo má ku každému dňu v týždni priradenú farbu: k pondelku modrú, k utorku zelenú, k strede bielu, k štvrtku červenú, k piatku oranžovú, k sobote sivú a k nedeli hnedú. V týchto farbách nosí aj ponožky, a to tak, že na pravej nohe má ponožku farby dňa, avšak na ľavej nohe nemá ponožku farby tohto dňa ani dňa nasledujúceho. (Napr. v sobotu má na pravej nohe sivú ponožku a na ľavej nemá sivú ani hnedú.)
Určte, ktorý je deň, ak mal Peťo na ľavej nohe predvčerom modrú ponožku, včera červenú a dnes má na nej hnedú.

Z6-I-6
Obdĺžnikový park má obvod 228 metrov. Vo vrcholoch obdĺžnika a na jeho stranách rástlo 38 okrasných kríkov tak, že vzdialenosti medzi každými dvoma susednými kríkmi boli rovnaké. Na dvoch protiľahlých stranách obdĺžnika zasadil záhradník medzi každé dva kríky jeden ďalší. Tým zvýšil počet kríkov po obvode parku na 60.
Určte rozmery parku.

Z6-II-1

Z6-II-2

Z6-II-3

Z7-I-1
Koľko štvorciferných čísel má tú vlastnosť, že ich tretina, polovica, dvojnásobok a trojnásobok sú tiež štvorciferné čísla?

Z7-I-2
V pravidelnom šesťuholníku ABCDEF je bod G stred uhlopriečky AE.
Určte pomer obsahov trojuholníka ADG a šesťuholníka ABCDEF.

Z7-I-3
Páni Komický, Elegantný a Vážny sa poznajú z golfu. Jeden sa volá Karol, jeden Erik a jeden Viktor. Jeden nosí kravatu krémovej farby, jeden ebenovej farby a jeden vínovej farby.

• Výherca posledného zápasu nosí kravatu ebenovej farby.
• Pán Elegantný nebol nikdy na návšteve u pána Komického.
• Viktor nosí krémovú kravatu.
• Pánovi Komickému pripadá vtipné, že nikdy nevyhral.
• Karol bol po poslednom stretnutí na návšteve u pána Komického.
• Pán Vážny nosí kravatu vínovej farby.

Zistite, aké je vlastné meno každého z pánov a kto nosí akú kravatu.

Z7-I-4
Adela, Beáta, Sárka a Julka si natrhali čerešne. Beáta ich mala 5-krát viac ako Adela, Sárka mala o 15 čerešní viac ako Beáta, Julka mala o 200 viac ako Adela.
Najmenej o koľko sa mohli líšiť počty čerešní Sárky a Julky? A koľko čerešní by v takom prípade malo každé z dievčat?

Z7-I-5
Václav mal niekoľko bielych kociek. Na každej kocke zafarbil tri rôzne steny troma rôznymi farbami, a to červenou, zelenou a modrou. Potom roztriedil kocky do skupín podľa typu zafarbenia tak, že do každej skupiny dal všetky kocky, ktoré vyzerali po vhodnom otočení rovnako.
Najviac koľko skupín mohol Václav vytvoriť?

Z7-I-6
Pre štvoruholník ABCD platí:

• strana AD a uhlopriečka BD sú rovnako dlhé,
• uhlopriečka BD a strana DC sú kolmé,
• strany AB a BC sú kolmé,
• os uhla BDC a strana AD sú kolmé.

Určte veľkosť uhla BCD.

Z7-II-1

Z7-II-2

Z7-II-3

Z8-I-1
Nájdite všetky trojice navzájom rôznych prvočísel (p, q, r), pre ktoré platí

Z8-I-2
Pre rovnobežníky ABCD a KLMN platí:

• bod K je stred úsečky CD,
• bod K je priesečník priamky CD s osou úsečky BC,
• bod L je priesečník priamky AB s osou úsečky CD,
• bod N je priesečník priamky AB s osou úsečky BC,
• uhol BAD má veľkosť 60°.

Určte pomer obsahov rovnobežníkov ABCD a KLMN.

Z8-I-3
Tomáš zbiera pohľadnice z Islandu, Anglicka a Nórska. Z každej krajiny má aspoň jednu pohľadnicu, celkovo ich má 40. Pohľadníc z Anglicka má viac ako pohľadníc z Nórska. Pohľadníc z Islandu má viac ako 5 násobok a menej ako 6 násobok počtu pohľadníc z Anglicka.
Z ktorých krajín sú pohľadnice, ktorých počet v Tomášovej zbierke je možné určiť jednoznačne?

Z8-I-4
Žiaci získali v prvej písomke priemerne 84 bodov. Tí istí žiaci napísali druhú písomku s priemerným ziskom 70 bodov. Štyria z týchto žiakov mali v oboch písomkách po 63 bodov. Priemerný zisk ostatných žiakov v druhej písomke bol 72 bodov.
Určte priemerný počet bodov ostatných žiakov v prvej písomke.

Z8-I-5
Je daná kružnica k so stredom S a polomerom 6 cm a priamka p prechádzajúca bodom S. Zostrojte obdĺžnik ABCD tak, aby platilo:

• vrcholy A a B ležia na priamke p,
• kružnica k sa dotýka strany CD,
• kružnica k pretína stranu AD v bode K a stranu BC v bode L,
• |AK| = |CL| = 1,5 cm.

Z8-I-6
Jonáš a Michal zostavili každý svoj 8-boký ihlan s 9 rôznymi číslami na jeho rôznych stenách. Všetky čísla boli väčšie ako 10 a menšie ako 30. Pre každý vrchol ihlana platilo, že súčet čísel na všetkých stenách obsahujúcich tento vrchol bol násobkom čísla 4, pritom žiadne číslo násobkom čísla 4 nebolo. Jonáš tvrdil, že na dvoch stenách má čísla 14 a 15. Michal tvrdil, že na dvoch stenách má čísla 14 a 17.
Mohli obidvaja chlapci hovoriť pravdu?

Z8-II-1

Z8-II-2

Z8-II-3

Z9-I-1
V rohových políčkach tabuľky 3 × 3 sú napísané čísla tak, ako na obrázku:

3		6
12		15

Do prázdnych políčok doplňte nenulové prirodzené čísla tak, aby súčin čísel v každom riadku a každom stĺpci bol rovnaký. Nájdite všetky možnosti.

Z9-I-2
Útvar na obrázku je vytvorený z piatich zhodných azúrových kosoštvorcov a jedného žltého pravidelného päťuholníka, ktorý kosoštvorce čiastočne prekrýva. Kosoštvorce susedia celými stranami a na týchto stranách ležia vrcholy päťuholníka. Pomer dĺžky polomeru kružnice opísanej päťuholníku a dĺžky strany kosoštvorca je 4 ∶ 7.

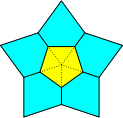
Rozhodnite, či neprekrytá časť každého kosoštvorca má väčší, rovnaký alebo menší obsah ako päťuholník.

Z9-I-3
Na tabuli je napísaných niekoľko po sebe nasledujúcich prirodzených čísel počnúc číslom 1. Každé z týchto čísel má buď azúrovú, alebo žltú farbu. Súčet každých dvoch rôznofarebných čísel je prvočíslo, súčet každých dvoch čísel rovnakej farby je zložené číslo.
Najviac koľko čísel môže byť napísaných na tabuli?

Z9-I-4
Nenulové prirodzené číslo nazveme kvadrátové, ak jeho zápis obsahuje cifru alebo skupinu po sebe idúcich cifier, ktoré sú zápisom druhej mocniny nenulového prirodzeného čísla. (Napr. čísla 257 a 725 sú kvadrátové, čísla 275 a 572 nie.)
Určte počet všetkých dvojciferných kvadrátových čísel.

Z9-I-5
V lyžiarskom oddiele sa počet všetkých detí znížil o 10 %, pričom pomer dievčat voči všetkým deťom vzrástol z 50 % na 55 %.
O koľko percent sa zmenil počet dievčat?

Z9-I-6
Kružnice k a l sa dotýkajú zvonku, pričom polomer kružnice k je rovnaký ako priemer kružnice l. Bod S je stred kružnice k, bod T je bod dotyku kružníc, bod A leží na kružnici l mimo spojnice stredov kružníc a bod M je stred úsečky AS.
Dokážte, že uhol ATM je pravý.

Z9-II-1

Z9-II-2

Z9-II-3

Z9-II-4

Z9-III-1

Z9-III-2

Z9-III-3

Z9-III-4

Uložiť

Uložiť