74. ročník matematickej olympiády 2024-2025
Súťažné úlohy kategórií Z5-Z9

aktualizované 03.11.2024 17:30

Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce
okresné	okresné	okresné	okresné	okresné
				krajské

Z5-I-1
Čapkovci majú dvoch synov, Karola a o dva roky staršieho Petra. Nemcovci majú dcéru Boženu. Všetky tri deti majú narodeniny v ten istý deň a obe rodiny ich vtedy oslavujú spoločne. Pri tohtoročnej oslave bola Božena trikrát staršia ako Karol. O tri roky budú mať Karol a Peter spolu toľko rokov ako Božena.
Koľko rokov mali deti pri tohtoročnej oslave?

Z5-I-2
Na obrázku je sivý štvorec so stranou dĺžky 10 cm. Štvorec dopĺňajú štyri rovnaké pravouhlé trojuholníky do tvaru hviezdy. Súčet obsahov týchto štyroch trojuholníkov je štvornásobkom obsahu štvorca.

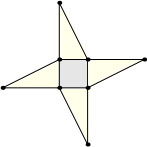
Určte dĺžku druhej najdlhšej strany každého z týchto štyroch trojuholníkov.

Z5-I-3
V nasledujúcom výraze je päťkrát použité znamienko + a jeho hodnota 39 je násobkom 3:

Zmeňte dve zo znamienok „+“ na znamienka „−“ tak, aby hodnota nového výrazu bola opäť násobkom 3. Nájdite všetky možnosti.

Z5-I-4
Pinocchio tvrdí, že číslo dňa v dátume jeho narodenia možno bezo zvyšku deliť 3, 4, 5 a 6. Tri z týchto štyroch informáciı́ sú pravdivé, jedna je nepravdivá.
Koľký deň v mesiaci môže mať Pinocchio narodeniny? Nájdite všetky možnosti.

Z5-I-5
V sieti chodníkov vyznačených na obrázku má každý chodník medzi susednými križovatkami dĺžku 1 km.

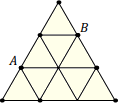
Koľko ciest dlhých nanajvýš 3 km vedie po chodníkoch z miesta 𝐴 do miesta 𝐵?

Z5-I-6
Anička navlieka na niť bezprostredne za seba koráliky troch rôznych tvarov A, B, C. Postupuje tak, že tvary strieda stále v rovnakom poradí a postupne zvyšuje počty tvarov v skupinách, a to takto:

Korálik tvaru A zaberá 5 mm nite, korálik tvaru B 4 mm, korálik tvaru C 3 mm.
Koľko korálikov potrebuje Anička na výrobu náhrdelníka dlhého aspoň 50 cm?

Z5-II-1
Janka a Danka jedli počas týždňa ovocie. Janka jedla len hrušky  alebo jablká, Danka jedla iba čerešne. Každý deň zjedla Janka najviac jeden kus ovocia a Danka jedla v ten istý deň čerešne podľa nasledujúceho rozpisu:

• Keď Janka zjedla hrušku, zjedla Danka dve čerešne.
• Keď Janka zjedla jablko, zjedla Danka tri čerešne.
• Keď Janka nezjedla žiadne ovocie, zjedla Danka šesť čerešnı́.

Od pondelka do nedele zjedla Danka dokopy 19 čerešnı́.
Koľko ktorého ovocia mohla zjesť za ten istý týždeň Janka? Nájdite obe možnosti.

Z5-II-2
Okružná cesta spája tri dediny tak ako na obrázku. Vo vyznačenom smere to je z Pávoviec do Krtkovian 10 km, z Mňaukova do Pávoviec 15 km a z Krtkovian do Mňaukova 16 km.

Aká dlhá je celá okružná cesta?

Z5-II-3
Z 2025 rovnakých štvorcov je zložený útvar podľa pravidla naznačeného na obrázku. Strana štvorca je 1 cm.

Určte obvod útvaru.

Z6-I-1
Pán Vaflička vypráža a predáva šišky, pán Šiška pečie a predáva vafle. Obaja cukrári majú každý týždeň otvorené od pondelka do piatka. Lenka u nich kupuje každý pondelok 2 vafle a 1 šišku, každý utorok 3 šišky a 1 vafľu, každú stredu 4 šišky, každý štvrtok 3 vafle a každý piatok 2 šišky a 2 vafle. Pán Šiška si raz všimol, že od prvého pondelka tohto mesiaca predal Lenke dokopy 30 vaflí. Koľko šišiek predal Lenke za rovnaké obdobie pán Vaflička?

Z6-I-2
V obdĺžniku so stranami dĺžok 4 cm a 8 cm ležia dve rôzne polkružnice, z ktorých každá má krajné body v jeho dvoch susedných vrcholoch a dotýka sa protiľahlej strany. Zostrojte štvorec taký, že jeho dva vrcholy ležia na jednej polkružnici, zvyšné dva na druhej a jeho strany sú rovnobežné so stranami obdĺžnika.

Z6-I-3
Päťciferný palindróm je také päťciferné číslo, ktoré má na mieste jednotiek rovnakú cifru ako na mieste desaťtisícok a na mieste desiatok rovnakú cifru ako na mieste tisícok. Nájdite najmenší päťciferný palindróm deliteľný číslom 36.

Z6-I-4
Šárka s Ľubošom spoločne zasadili 70 tulipánov rôznych farieb. Šárka nesadila žlté tulipány a päť devätín tulipánov, ktoré zasadila, boli červené. Ľuboš nesadil červené tulipány a dve sedemnástiny tulipánov, ktoré zasadil, boli žlté. Koľko zasadených tulipánov malo inú farbu ako červenú alebo žltú?

Z6-I-5
Tri kamarátky sa po rokoch zišli a rozprávali sa o tom, kde ktorá z nich býva:
Prvá: „Ja bývam v Hruštíne.“.
Druhá: „Ja nebývam v Očovej.“.
Tretia druhej: „Ty nebývaš v Jasenove.“.
Kamarátky naozaj bývajú v spomínaných dedinách, každá v inej. Jedna z kamarátok nepovedala pravdu a nebola to tá z Očovej.
Rozhodnite, kde ktorá z kamarátok býva.

Z6-I-6
V štvorcovej sieti sú tri kruhy a tri trojuholníky, každý v inom políčku. Každý útvar má aspoň jedného suseda, pričom susedia sú políčka so spoločnou stranou. Obsadené políčka tvoria súvislú oblasť, t. j. od každého ku každému sa dá dostať cez susedov. Každú noc sa každý útvar môže zmeniť podľa toho, ako cez deň vyzerali jeho susedia:

• Ak je útvar kruh a medzi jeho susedmi bolo viac trojuholníkov ako kruhov, tak sa zmení na trojuholník.
• Ak je útvar trojuholník a medzi jeho susedmi bolo viac kruhov ako trojuholníkov, tak sa zmení na kruh.
• V ostatných prípadoch sa ú tvar nezmení.

Príklad štvorcovej siete a premeny jej útvarov po jednej noci je na obrázku:

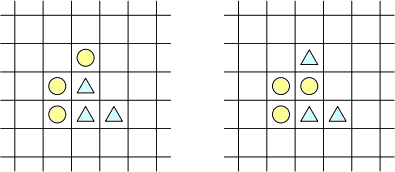
Nájdite aspoň jedno rozmiestnenie troch kruhov a troch trojuholníkov do siete také,
a) aby sa v noci nezmenili;
b) aby sa každý útvar každú noc zmenil;
c) aby po niekoľkých nociach boli všetky útvary rovnaké.

Z6-II-1
Prirodzené čı́slo nazveme pekné, ak je väčšie ako 7000 a súčin jeho cifier je 252.
Nájdite dve najmenšie pekné čı́sla.

Z6-II-2
Cestičky medzi úkrytmi cvrčkov Adama, Borisa, Cyrila, Daniela a Erika tvoria sieť ako na obrázku a ich ú kryty sú označené prvými pı́smenami ich mien. Pritom platı́:

• Cestičky medzi ú krytmi Adama, Borisa a Erika tvoria rovnostranný trojuholnı́k.
• Cestičky medzi úkrytmi Borisa, Cyrila, Daniela a Erika tvoria obdĺžnik s obsahom 360 dm².
• Prechádzka po cestičkách od Adama k Borisovi, Cyrilovi, Danielovi, Erikovi a Adamovi je o 24 dm dlhšia ako prechádzka od Adama k Borisovi, Erikovi a Adamovi.

Aká dlhá je cestička medzi úkrytmi Adama a Erika?

Z6-II-3
Jakub prečı́tal knihu počas troch dnı́. V utorok prečı́tal tretinu všetkých strán, v stredu prečı́tal tri sedminy zvyšných strán a posledných 32 strán prečı́tal vo štvrtok.
Koľko strán mala kniha?

Z7-I-1
Alenka a Zuzka jedli slivky. Prvý deň zjedla Alenka tri štvrtiny toho, čo v ten istý deň zjedla Zuzka. Druhý deň zjedla Zuzka tri polovice toho, čo v ten istý deň zjedla Alenka. Dokopy za oba dni zjedli 31 sliviek a každé dievča každý deň zjedlo celočíselný počet sliviek. Koľko sliviek zjedla za oba dni Alenka?

Z7-I-2
Mikuláš postavil pyramídu zo 6 rovnakých kociek s hranami dĺžky 7 cm. Spodné poschodie tvorili 3 kocky, prostredné poschodie 2 kocky a horné poschodie 1 kocka. Susedné kocky v každom poschodí mali spoločnú stenu, poschodia navzájom neprečnievali. Víťazoslav posunul kocky tak, že každá kocka v horných dvoch poschodiach stála na dvoch spodných kockách a medzi susednými kockami v spodných dvoch poschodiach boli medzery široké tretinu hrany kocky. Až na tieto medzery poschodia navzájom neprečnievali. O koľko cm² sa líšia povrchy pôvodnej a upravenej pyramídy?

Z7-I-3
Pankrác, Servác a Bonifác sa ubytovali v hoteli. Čísla izieb boli trojciferné a cifra na mieste stoviek určovala poschodie, na ktorom sa izba nachádzala. Na raňajkách si podľa príveskov na kľúčoch od izieb všimli, že:

• v číslach ich izieb sú použité všetky cifry od 1 do 9,
• Pankrácovo číslo je deliteľné 9, Servácovo číslo je deliteľné 8, Bonifácovo číslo je deliteľné 7,
• Bonifácovo číslo je 4 krá t väčšie ako Pankrácovo číslo,
• Servác býva na poschodí medzi Pankrácom a Bonifácom.

Určte čísla izieb Pankráca, Serváca a Bonifáca.

Z7-I-4
V jednej z piatich nádob očíslovaných 1, 2, 3, 4, 5 je minca. Sprievodné nápisy oznamujú:

• „Minca je v nádobe s nepárnym číslom.“,
• „Minca je v nádobe s číslom väčším ako 3.“,
• „Minca je v nádobe s číslom menším ako 4.“.

Čestný strážca s bezchybným úsudkom dodáva: „Jeden z nápisov nie je pravdivý, zvyšné dva pravdivé sú. Hoci viem, ktorý nápis pravdivý nie je, neviem určiť, v ktorej nádobe je minca.“. Rozhodnite, ktorý z nápisov nie je pravdivý.

Z7-I-5
Nech 𝐴𝐵𝐶 je trojuholník taký, že |𝐴𝐵| = 6 cm, |𝐵𝐶| = 8 cm a |𝐴𝐶| = 12 cm.
Zostrojte polkružnicu takú, že sa dotýka strán 𝐴𝐵 a 𝐵𝐶 a jej krajné body ležia na strane 𝐴𝐶.

Z7-I-6
Katka a Števo pečú každý na svojej panvici bez prestávok jednu palacinku za druhou a hotové palacinky dávajú na spoločný tanier. Obaja začali piecť súčasne. Katke trvá každá palacinka 3 minúty, Števovi trvá každá palacinka 4 minúty. Každých 5 minút od začiatku pečenia sa objaví maškrtný kocúr Lucifer. Ak sa Katka i Števo venujú pečeniu, tak im Lucifer jednu hotovú palacinku ukradne. Ak niekto z nich práve dáva palacinku z panvice na tanier, tak sa schová a palacinku neukradne.
Koľko palaciniek musia Katka so Števom upiecť, aby im ich ostalo 150? Ako dlho im to bude trvať?

Z7-II-1
Mamička si nachystala pernı́čky na zdobenie. Každý pernı́ček zdobı́ rovnako dlho. Keby pri zdobenı́ každého pernı́čka bola o jednu minútu rýchlejšia, mohla by skončiť o 48 minút skôr alebo by v takto ušetrenom čase mohla ozdobiť (v novom zrýchlenom tempe) presne 12 ďalšı́ch pernı́čkov.
Koľko pernı́čkov si mamička nachystala a ako dlho jej bude trvať ich zdobenie (v pôvodnom nezrýchlenom tempe)?

Z7-II-2
V útulku je 60 zvierat, a to výhradne mačky a psy. Tretina mačiek a tri osminy psov nie sú ani rok staré, 39 zvierat má rok alebo viac.
Koľko je v útulku mačiek a koľko psov?

Z7-II-3
Kosoštvorec 𝐴𝐵𝐶𝐷 je zložený z rovnobežnı́kov s navzájom rovnakými obsahmi. Vyznačená spoločná strana 𝑇𝑈 dvoch rovnobežnı́kov má dĺžku 2 cm.
Určte obvod kosoštvorca 𝐴𝐵𝐶𝐷.

Z8-I-1
Ivan, Jaro, Karol a Ľuboš majú dokopy 90 známok. Keby mal Ivan o dve známky menej, Jaro o dve viac, Karol dvojnásobok a Ľuboš polovicu toho, čo teraz, mali by všetci rovnako. Koľko známok má každý z chlapcov?

Z8-I-2
Nájdite aspoň jedno rozdelenie rovnoramenného trojuholníka so základňou dĺžky 12 cm a výškou na základňu dĺžky 18 cm na tri lichobežníky s rovnakým obsahom.

Z8-I-3
Čísla a, b, c, d sú také, že platí:

• Číslo a dáva po delení 3 zvyšok 1.
• Číslo b dáva po delení 6 zvyšok 2.
• Platí a − b = d − c.
• Číslo d je deliteľné 3.

Aký zvyšok po delení 9 môže dávať číslo c? Nájdite všetky možnosti.

Z8-I-4
Nech 𝐴𝐵𝐶𝐷𝐸 je pravidelný päťuholník. Rovnobežka s priamkou 𝐴𝐵 prechádzajúca bodom 𝐶 pretína priamku 𝐵𝐷 v bode 𝐹. Kolmica na priamku 𝐶𝐹 prechádzajúca bodom 𝐶 pretína priamku 𝐵𝐷 v bode 𝐺.
Určte veľkosť uhla 𝐴𝐺𝐹.

Z8-I-5
Určte všetky možné dvojice čísel (a, b) také, že podiel najmenšieho spoločného násobku a najväčšieho spoločného deliteľa čísel a a b je 75 a súčet čísel a a b je väčší ako 100 a menší ako 200.

Z8-I-6
Rybár Šťuka chytil niekoľko rýb. Keď predal tri najťažšie ryby majiteľovi miestnej reštaurácie, znížil celkovú hmotnosť svojho úlovku o 35 %. Keď dal tri najľahšie ryby svojmu psovi, znížil hmotnosť zostávajúcich ulovených rýb o päť trinástin.
Koľko rýb chytil pán Šťuka?

Z8-II-1
Kúzelnı́kov povraz je dlhšı́ ako 10 m. Nech by rozdelil povraz na dve časti v hociktorom z troch pomerov 3 ∶ 5, 7 ∶ 11, 13 ∶ 17, boli by dĺžky oboch častı́ vyjadrené v centimetroch zakaždým prirodzeným čı́slom.
Aká je najmenšia možná dĺžka kúzelnı́kovho povrazu?

Z8-II-2
Monika si vybrala dve čı́sla, aby preskúšala schopnosti robota Popletu. Najprv mu dala sčı́tať obe čı́sla. Popletov výsledok bol o 4,1 menšı́ ako výsledok pri správnom sčı́tanı́. Potom mu dala sčı́tať trojnásobok prvého čı́sla s druhým čı́slom. Teraz bol Popletov výsledok o 8,4 menšı́ ako výsledok pri správnom sčı́tanı́. Čoskoro zistila, že Popleta nepočı́ta súčet dvoch zadaných čı́sel, ale správne vypočı́ta ich aritmetický priemer.
Ktoré čı́sla si Monika vybrala?

Z8-II-3
V trojuholnı́ku 𝐴𝐵𝐶 ležı́ bod 𝐷 na strane 𝐵𝐶 a bod 𝐸 na strane 𝐴𝐶 tak, že platı́

Určte veľkosti uhlov 𝐴𝐶𝐵 a 𝐵𝐴𝐷.

Z9-I-1
Nájdite všetky dvojice celých čísel (𝑥, 𝑦) také, že 𝑥 + 𝑦 je prvočíslo a 3𝑥 + 5𝑦 = 16.

Z9-I-2
Pravidelný štvorboký hranol má objem 864 cm³ a obsah jeho plášťa je dvojnásobkom obsahu jeho podstavy. Určte veľkosť jeho telesovej uhlopriečky.

Z9-I-3
Nájdite najväčšie možné 𝑛, pre ktoré je možné množinu {1, 2, … , 𝑛} rozdeliť do 5 neprázdnych podmnožín tak, aby čísla v každej podmnožine boli po dvoch nesúdeliteľné.

Z9-I-4
Rozhodnite, či je možné k číslu s ciferným súčtom 2024 pripočítať jednociferné číslo tak, aby výsledné číslo malo ciferný súčet 74.

Z9-I-5
Nech 𝐴𝐵𝐶 je trojuholník taký, že strana 𝐴𝐵 je dvakrát dlhšia ako strana 𝐴𝐶 a os uhla 𝐵𝐴𝐶 pretína stranu 𝐵𝐶 v bode 𝐷. Nech rovnobežka so stranou 𝐴𝐵 prechádzajúca bodom 𝐷 pretína stranu 𝐴𝐶 v bode 𝐸 a rovnobežka s úsečkou 𝐴𝐷 prechádzajúca bodom 𝐸 pretína stranu 𝐵𝐶 v bode 𝐹.
Určte pomer dĺžok úsečiek 𝐴𝐷 a 𝐸𝐹.

Z9-I-6
Plavci Pstruh a Kapor si chceli zmerať svoje sily. Z protiľahlých strán bazéna skočili súčasne do susedných dráh a plávali proti sebe, každý svojou konštantnou rýchlosťou. Prvýkrát sa plavci minuli vo vzdialenosti 8 metrov od Pstruhovej štartovacej strany, na konci dráhy sa rýchlo otočili a plávali naspäť. Druhýkrát sa plavci minuli vo vzdialenosti 5 metrov od Kaprovej štartovacej strany, doplávali na koniec dráhy, a tým sa preteky skončili.
Určte, kto vyhral a aká bola dĺžka bazéna.

Z9-II-1
Nájdite všetky dvojciferné prirodzené čı́sla, ktoré majú nasledujúcu vlastnosť: Keď pred čı́slo pripı́šeme súčin jeho prvej cifry a jeho prvej cifry zväčšenej o 1, dostaneme druhú mocninu
pôvodného čı́sla.

Z9-II-2
Nájdite všetky trojice navzájom rôznych čı́sel takých, že:

• jedno z nich je aritmetickým priemerom zvyšných dvoch,
• súčet aritmetického priemeru najväčšieho a stredného čı́sla a aritmetického priemeru stredného a najmenšieho čı́sla je 628 a rozdiel týchto dvoch aritmetických priemerov je 83.

Na poradı́ čı́sel v trojici nezáležı́.

Z9-II-3
Včera vydojili na farme Doj dvakrát viac mlieka ako na farme Hoj a na farme Loj dvakrát viac mlieka ako na farme Doj. Každá farma poslala časť vydojeného mlieka na výrobu masla. Farma Doj poslala na výrobu masla 7/8 svojho mlieka a farma Hoj 3/4 svojho mlieka. Z mlieka vydojeného na všetkých troch farmách išlo na výrobu masla dokopy 90 %.
Akú časť svojho mlieka poslala na výrobu masla farma Loj?

Z9-II-4
Obdĺžnik ABCD má obsah 82 cm². Bod E je stredom strany CD a bod P je priesečnı́kom úsečiek AC a BE.
Určte obsah trojuholnı́ka ABP.

Z9-III-1

Z9-III-2

Z9-III-3
(Karel Pazourek)

Z9-III-4

Uložiť

Uložiť