aktualizované 08.07.2023 22:40

Z5	Z6	Z7	Z8	Z9
domáce	domáce	domáce	domáce	domáce
okresné	okresné	okresné	okresné	okresné
				krajské

Z5-I-1
Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15 dm, a keď sa odrazil oboma nohami, skočil 61 dm. Koľko skokov zajac urobil, kým dorazil do cieľa? Ktorou nohou sa odrazil pri cieľovom skoku?

Z5-I-2
Zuzka postavila zo šestnástich rovnako veľkých kociek kváder s pôdorysom 4 × 4. S ďalšími rovnako veľkými kockami pokračovala v stavaní. Kocky ukladala tak, že každé dve susedné mali spoločnú celú stenu. Výsledná stavba vyzerala z dvoch rôznych strán ako na nasledujúcom obrázku. Zistite, koľko najviac a koľko najmenej kociek mohla Zuzka na svoju stavbu použiť.

Z5-I-3
Katka mala v záhradke päť záhonov rozmiestnených ako na obrázku. Do záhonov chcela zasadiť cesnak, mrkvu a reďkvičku tak, aby na každom záhone bol len jeden druh zeleniny a aby žiadne dva záhony s rovnakou zeleninou nesusedili. Koľkými rôznymi spôsobmi mohla Katka do záhonov zasadiť cesnak, mrkvu a reďkvičku?

Z5-I-4
V záhradkárskej osade mal pán Jahoda vo svojom sude 16 litrov vody. Sused pán Malina mal vo svojom sude trikrát viac vody ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vody ako pán Jahoda. Koľko litrov vody napršalo do každého suda?

Z5-I-5
Zo štyroch zhodných štvorcov bol vytvorený ornament ako na obrázku.

Strany štvorcov sú dlhé 4 cm, sú navzájom rovnobežné alebo kolmé a pretínajú sa buď vo svojich štvrtinách, alebo poloviciach. Libor chcel ornament vyfarbiť a zistil, že farba na 1 cm2 každého súvislého poľa ho bude stáť toľko eur, koľkým štvorcom je toto pole spoločné. Koľko eur bude stáť farba na vyfarbenie celého ornamentu?

Z5-I-6
Lucka napísala na lístok číslo 12345 a dvakrát ho medzi ciframi rozstrihla. Získala tak tri menšie kartičky s tromi číslami. Tieto kartičky zoradila dvoma spôsobmi, čím dostala dve rôzne päťciferné čísla. Rozdiel týchto dvoch čísel bol 28 926. Medzi ktorými ciframi Lucka lístok rozstrihla?

Z5-II-1
Deti dostali úlohu s piatimi prázdnymi políčkami:

Do každého políčka mali vpísať jedno z čísel 1, 2, 3, 4, 5 tak, aby každé číslo použili iba raz a aby delenie vychádzalo bezo zvyšku.
Nájdite všetky výsledky, ktoré mohli deti dostať.

Z5-II-2
Albert, Ben, Cyril, Daniel, Erik, Filip a Gabriel vstúpili v tomto poradí po jednom za sebou do jaskyne so sto dverami. Svoje poradie menia len pri prechode dverami, a to takto: Prvý zo zástupu otvorí dvere, podrží ich všetkým ostatným a potom sa zaradí na koniec. Prvé dvere teda otvára Albert, druhé Ben a tak ďalej.
Kto otvorí sté dvere?

Z5-II-3
Na obraze sú dva biele štvorce v sivom poli. Strany obrazu a strany oboch štvorcov sú orientované vodorovne alebo zvisle:

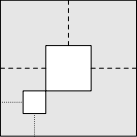
Bodkovane vyznačené vzdialenosti menšieho štvorca od strán obrazu sú rovnaké ako veľkosť strany tohto menšieho štvorca. Čiarkovane vyznačené vzdialenosti väčšieho štvorca od strán obrazu sú rovnaké ako veľkosť strany tohto väčšieho štvorca. Obsah sivej časti obrazu je 62 cm² .
Určite obsah bielej časti obrazu.

Z6-I-1
Kamaráti Jaro, Pavol a Rasťo hrali guľôčky. Jarovi sa veľmi nedarilo, takže mal po hre najmenej guľôčok zo všetkých. Chlapcom to bolo ľúto, preto dal Rasťo Jarovi polovicu všetkých svojich guľôčok a Pavol tretinu tých svojich. Teraz mal najviac guľôčok Jaro, a tak svojim dvom kamarátom vrátil každému sedem guľôčok. Po týchto výmenách mali všetci rovnako, a to po 25 guľôčok. Koľko guľôčok mal po hre (pred výmenami) Jaro?

Z6-I-2
Karolína narysovala štvorec so stranou 6 cm. Na každej strane štvorca vyznačila modrou farbou dva body, ktorý mi rozdelila príslušnú stranu na tri zhodné časti. Potom zostrojila štvoruholník, ktorý mal všetky vrcholy modrej farby a ktorého žiadne dva vrcholy neležali na rovnakej strane štvorca. Aké obsahy štvoruholníkov mohla Karolína dostať? Nájdite všetky možnosti.

Z6-I-3
V osemcifernom čísle je každá jeho cifra (okrem poslednej) väčšia ako nasledujúca cifra. Koľko je všetkých takýchto čísel?

Z6-I-4
V nasledujúcom písomnom násobení dvoch trojciferných čísel sú cifry zastúpené hviezdičkami. Na miesta hviezdičiek doplňte cifry tak, aby bol výpočet správny:

Z6-I-5
Z navzájom zhodných trojuholníkov je zložených niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Vypočítajte obvod štvrtého útvaru.

Z6-I-6
Alex, Barbora, Cyril, Dana, Eva, František a Gabika sa stali na svojich školách víťazmi v stolnom tenise a zišli sa na dvojdňovom turnaji o celkového víťaza. Každé z týchto siedmich detí malo počas turnaja zohrať jeden zápas s každým iným. Prvý deň turnaja hral Alex jeden zápas, Barbora hrala dva zápasy, Cyril tri, Dana štyri, Eva päť zápasov a František šesť. Koľko zápasov hrala prvý deň Gabika?

Z6-II-1
Žiaci dostali prirodzené číslo menšie ako 100. Alex dané číslo zaokrúhlil na desiatky. Barbora dané číslo zaokrúhlila na stovky. Cyril dané číslo vynásobil dvoma. Dana zaokrúhlené Alexovo číslo a Barborino číslo sčítala. Eva od Daninho čísla odpočítala Cyrilovo číslo. František oznámil Evin výsledok a ten bol 30.
Ktoré číslo mohli žiaci na začiatku dostať? Určte všetky možnosti.

Z6-II-2
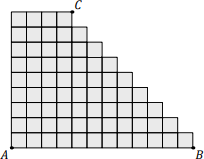
Zo zhodných štvorcov so stranou dĺžky 1 cm je zložený útvar s nasledujúcimi vlastnosťami:

• Útvar je tvorený radmi susediacich štvorcov.
• Spodný rad pozostáva z 12 štvorcov.
• Každý vyšší rad začína zľava rovnako ako rad pod ním, má však o jeden štvorec menej.
• Horný rad tvoria 4 štvorce.

Vrcholy spodnej strany útvaru sú označené 𝐴 a 𝐵, pravý vrchol hornej strany je označený 𝐶. Určte obsah trojuholníka 𝐴𝐵𝐶.

Z6-II-3
V krajine Binária žijú matematici niekoľkých úrovní. Všetci matematici rovnakej úrovne vyriešia za deň rovnaký počet úloh. Matematik vyššej úrovne vyrieši za deň dvojnásobné množstvo úloh ako matematik predchádzajúcej úrovne (teda napríklad matematik štvrtej úrovne vyrieši za deň dvakrát viac úloh ako matematik tretej úrovne).
Traja matematici piatej úrovne vyriešia za deň o tisíc úloh viac ako štyria matematici druhej úrovne.
Koľko úloh vyrieši za deň jeden matematik druhej úrovne?

Z7-I-1
Ajka, Barborka, Cilka a Daniel sa dohadovali o počte zrniek piesku na ich pieskovisku. Daniel povedal kamarátkam svoj odhad a tie sa ho rozhodli overiť. Ajka narátala 873 451 230, Barborka 873 451 227 a Cilka 873 451 213 zrniek piesku. Súčet (kladných) rozdielov týchto troch výsledkov od Danielovho odhadu bol 29. Koľko zrniek piesku mohol odhadnúť Daniel? Uveďte všetky možnosti.

Z7-I-2
Pán Delfín a pán Žralok boli zdatní rybári. Raz dokopy ulovili 70 rýb. Medzi rybami, ktoré ulovil pán Delfín, bolo 5/9 pstruhov. Medzi rybami, ktoré ulovil pán Žralok, boli 2/17 kaprov. Koľko rýb ulovil pán Delfín?

Z7-I-3
Myslím si tri čísla. Keď ich sčítam, dostanem 15. Keď od súčtu prvých dvoch čísel odčítam tretie, dostanem 10. Keď od súčtu prvého a tretieho čísla odčítam druhé, dostanem 8. Ktoré čísla si myslím?

Z7-I-4
Anetkin strýko má narodeniny v ten istý deň v roku ako Anetkina teta. Strýko je starší ako teta, nie však o viac ako desať rokov, a obaja sú plnoletí. Na poslednej oslave si Anetka uvedomila, že keď vynásobí ich oslavované veky a výsledný súčin ešte vynásobí počtom psov, ktorí sa na oslave zišli, dostane číslo 2024. Koľko psov mohlo byť na tejto oslave? Určte všetky možnosti.

Z7-I-5
Pravouhlý trojuholník má obsah 36 m². V ňom je umiestnený štvorec tak, že dve strany štvorca sú časťami dvoch strán trojuholníka a jeden vrchol štvorca je v tretine najdlhšej strany. Určte obsah tohto štvorca.

Z7-I-6
Trpaslíci počítajú svoje veky v dňoch, takže každý deň oslavujú narodeniny. U trpaslíka Nošteka sa zišlo sedem trpaslíkov s vekmi 105, 120, 140, 168, 210, 280 a 420 dní. Počas oslavy sa všetkým ôsmim trpaslíkom podarilo rozdeliť do dvoch skupín s rovnakými súčtami vekov. Koľko najmenej a koľko najviac dní mohol mať trpaslík Noštek?

Z7-II-1
Deti hádzali klasickou hracou kockou s číslami od 1 do 6. Keď padlo párne číslo, tak zatlieskali. Keď padlo číslo deliteľné tromi, tak zadupali. Keď nastali oba prípady, urobili oboje, v ostatných prípadoch nerobili nič. Počas piatich hodov deti celkom trikrát zatlieskali a trikrát zadupali. Súčet čísel, ktoré postupne padli, bol 20.
Nájdite všetky možné pätice čísel, ktoré mohli padnúť, bez ohľadu na ich poradie.

Z7-II-2
Zo zhodných štvorcov so stranou dĺžky 1 cm je zložený útvar s nasledujúcimi vlastnosťami:

• Spodný a horný rad pozostáva z jedného štvorca.
• Ostatné rady majú po dvoch susediacich štvorcoch.
• Všetky stĺpce sú tvorené dvoma susediacimi štvorcami.
• Obvod útvaru je 178 cm.

Vrcholy spodnej strany útvaru sú označené 𝐴 a 𝐵, pravý vrchol hornej strany je označený 𝐶. Určte obsah trojuholníka 𝐴𝐵𝐶.

Z7-II-3
Na pretekoch sa spolu stretlo päť detí, dievčatá Anna a Fiona a chlapci Jurko, Lukáš a Tomáš. O cieľovom poradí máme tieto informácie:

• Žiadne dve deti sa neumiestnili na rovnakom mieste.
• Priemerné umiestnenie dievčat bolo rovnaké ako priemerné umiestnenie chlapcov.
• Obe dievčatá sa umiestnili pred Tomášom.
• Jurko sa umiestnil medzi Annou a Lukášom.

Určite cieľové poradie detí.

Z8-I-1
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10 %, pričom počet chlapcov sa zväčšil o 5 % a počet dievčat sa zväčšil o 20 %.
Koľko detí máme tento rok v oddiele?

Z8-I-2
Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kúskov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračoval ďalej: každý novovzniknutý kúsok roztrhal buď na štyri, alebo na desať menších kúskov. Rozhodnite a vysvetlite, či môže Adam týmto spôsobom natrhať presne 20 000 kúskov.

Z8-I-3
V športovom areáli tvorili stanovištia vrcholy pravidelného päťuholníka 𝐴𝐵𝐶𝐷𝐸. Tieto stanovištia boli pospájané priamymi cestami. Na ceste z 𝐴 do 𝐵 bola fontána 𝐹, ktorú so stanovišťom 𝐶 spájala cesta kolmá na cestu z 𝐵 do 𝐸. Pat a Mat sa zišli na stanovišti 𝐸 a rozhodli sa zamiesť niektoré cesty. Pat pozametal cestu z 𝐸 do 𝐵. Mat pozametal cestu z 𝐸 do 𝐴 a ešte z 𝐴 do 𝐹.
Určte, ktorý z nich zametal dlhší úsek.

Z8-I-4
Hynek napísal nasledujúci súčet s piatimi záhadnými sčítancami:

Prezradil, že znaky @, #, ∗, &, $ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný jedenástimi.
Ktoré najmenšie a ktoré najväčšie číslo môže byť výsledkom Hynkovho súčtu?

Z8-I-5
Trojuholník 𝐴𝐵𝐶 je rozdelený úsečkami ako na obrázku. Úsečky DE a AB sú rovnobežné. Trojuholníky 𝐶𝐷𝐻, 𝐶𝐻𝐼, 𝐶𝐼𝐸, 𝐹𝐼𝐻 majú rovnaký obsah, a to 8 dm². Zistite obsah štvoruholníka AFHD.

Z8-I-6
Adam vpı́sal do tabuľky 3 × 3 čísla od 1 po 9 ako na obrázku:

7	6	4
1	2	8
9	3	5

Pre toto vyplnenie platí, že súčet čísel troch políčok pozdĺž každej strany je stále rovnaký. Adam zistil, že čísla do tabuľky je možné vyplniť aj inak, bez toho, aby pokazil vlastnosť s rovnakými súčtami pozdĺž strán. Akú najmenšiu hodnotu môže mať tento súčet? Uveďte príklad tabuľky s najmenším súčtom pozdĺž strán a vysvetlite, prečo menšı́ súčet byť nemôže.

Z8-II-1
Počítačový program vypisoval po riadkoch čísla tvorené ciframi od 1 do 9. Cifry boli použité opakovane v prirodzenom poradí. Na každom riadku bolo o jednu cifru viac ako na riadku predchádzajúcom, na prvom riadku bola 1:

1 12 123 ⋮ 123456789 1234567891 12345678912 ⋮

Výpis bol ukončený číslom na 2024. riadku.
Zistite, na koľkých riadkoch boli čísla deliteľné
a) tromi,
b) štyrmi.

Z8-II-2
Medzi hračkami v obchode sú iba lode a autá. Lode tvoria štvrtinu hračiek. 75 % lodí a 40 % áut je červených. Červených hračiek je o 10 menej ako tých s inou farbou.
Koľko hračiek je v obchode?

Z8-II-3
Zostrojte deltoid ABCD so stranami AB a AD dĺžky 11 cm, stranami CB a CD dĺžky 6 cm a uhlopriečkou AC dĺžky 15 cm. Nájdite aspoň jedno jeho rozdelenie na štyri štvoruholníky tak, aby dva z nich boli deltoidy a druhé dva zhodné kosoštvorce. Konštrukciu opíšte a zdôvodnite.
(Deltoidom nazývame taký konvexný štvoruholník, ktorý má dve dvojice zhodných susedných strán.)

Z9-I-1
Pat a Mat si dali preteky v behu do svojej chalúpky. V istom okamihu platilo, že keby Mat mal zdolanú polovicu vzdialenosti, ktorú doteraz ubehol, chýbal by mu do chalúpky trojnásobok tejto polovičnej vzdialenosti. V tom istom okamihu platilo, že keby Pat mal zdolaný dvojnásobok vzdialenosti, ktorú doteraz ubehol, chýbala by mu do chalúpky tretina tejto dvojnásobnej vzdialenosti.
Kto bol v danom okamihu bližšie k chalúpke?

Z9-I-2
Zostrojte kosoštvorec 𝐴𝐵𝐶𝐷 taký, že platí |𝐴𝐶| = 8 cm a |𝐴𝑆| = 7 cm, kde 𝑆 je stredom strany 𝐶𝐷.

Z9-I-3
V základnej škole, kam chodí aj Žigmund, každoročne organizujú vedomostnú súťaž, v ktorej každý súťažiaci môže získať najviac 15 bodov. Tento rok bol priemerný bodový zisk súťažiacich zaokrúhlený na desatiny rovný 10,4. Žigmund si po súťaži uvedomil, že niektoré otázky si zle prečítal a odpovedal na niečo iné. Mohol tak mať o 4 body viac a priemerný bodový zisk zaokrúhlený na desatiny by sa tým zvýšil na 10,6.
Určte, koľko najmenej a koľko najviac detı́ mohlo tento rok súťažiť.

Z9-I-4
Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menšı́ ako správny výsledok.
Koľko malo Karolovi správne vyjsť?

Z9-I-5
Trojuholnı́k 𝐴𝐵𝐶 je pravouhlý s pravým uhlom pri vrchole 𝐶. Body 𝐴′ , 𝐵′ , 𝐶′ sú obrazy bodov 𝐴, 𝐵, 𝐶 postupne v stredových súmernostiach so stredmi 𝐶, 𝐴, 𝐵. Dokážte, že platí

Z9-I-6
Určte počet štvorcov, ktorých všetky vrcholy sú mrežovými bodmi štvorcovej siete pozostávajúcej zo 4 riadkov a 2023 stĺpcov.

Z9-II-1
Na prehliadke v miestnosti múzea bola skupina chlapcov a dievčat. Po prehliadke odišlo 15 dievčat, a v miestnosti tak zostalo dvakrát viac chlapcov ako dievčat. Následne odišlo 45 chlapcov, a v miestnosti tak zostalo päťkrát viac dievčat ako chlapcov.
Koľko dievčat bolo v miestnosti múzea počas prehliadky?

Z9-II-2
Obdĺžnik na obrázku je rozdelený na dva zhodné štvorce, štyri zhodné menšie pravouhlé trojuholníky a štyri zhodné väčšie pravouhlé trojuholníky. Veľkosti niektorých strán sú vyznačené na obrázku.

Vypočítajte rozmery obdĺžnika.

Z9-II-3
Iveta postupne vypisovala prirodzené čísla tvorené číslicami 1, 3, 5, 7. Žiadne iné číslice nepoužila, postupovala vzostupne od najmenšieho čísla a žiadne číslo nezabudla. Čísla písala bezprostredne za sebou, čím zostavila jedno mimoriadne dlhé číslo:

Ktorá číslica je v tomto čísle na 1286. mieste?

Z9-II-4
V piatich vrecúškach je spolu 52 guľôčok. V žiadnych dvoch vrecúškach nie je rovnaký počet guľôčok, niektoré vrecúško môže byť i prázdne. Všetky guľôčky z akéhokoľvek (neprázdneho) vrecúška je možné premiestniť do ostatných štyroch vrecúšok tak, že v nich budú rovnaké počty guľôčok.
a) Nájdite nejaké rozdelenie guľôčok do vrecúšok, ktoré má všetky uvedené vlastnosti.
b) Ukážte, že pri akomkoľvek rozdelení s uvedenými vlastnosťami je v niektorom vrecúšku práve 12 guľôčok.

Z9-III-1
V základnej škole, kam chodí aj Lukáš, organizujú vedomostnú súťaž s vopred zoradenými úlohami. Každá správne vyriešená úloha je hodnotená toľkými bodmi, aké je jej poradie. Každá neriešená či nie celkom správne vyriešená úloha je hodnotená 0 bodmi. Lukáš správne vyriešil len prvých 12 úloh. Ak by správne vyriešil len posledných 12 úloh, získal by o 708 bodov viac.
Koľko bolo súťažných úloh?

Z9-III-2
Nech ABC je trojuholník a D priesečník osí jeho vnútorných uhlov. Nech DEF, DGH, DIJ sú rovnostranné trojuholníky také, že vrcholy A, B, C sú postupne stredy strán EF, GH, IJ a body E, G, I ležia postupne v uhloch CDA, ADB, BDC. Veľkosť uhla EDJ je 51°, veľkosť uhla HDI je 66°.

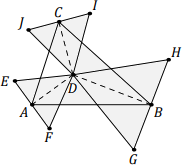
Určte veľkosti vnútorných uhlov trojuholníka ABC.

Z9-III-3
Na stranách trojuholníka ABC sú dané body D, E, F, G, H také, že platí:

• bod D je stredom strany AC,
• bod E je stredom strany BC,
• body F a G ležia postupne na úsečkách CD a CE tak, že FG ∥ DE,
• bod H leží na úsečke AB tak, že |AH| ∶ |AB| = 3 ∶ 7,
• pomer obsahov mnohouholníkov DEGF a DHEGF je 3 ∶ 7.

Určte pomer veľkostí úsečiek FG a DE.

Z9-III-4
Nájdite všetky trojice trojciferných prirodzených čísel (a, b, c) také, že

Uložiť

Uložiť