67. ročník matematickej olympiády 2017-2018
Súťažné úlohy kategórií A, B a C

aktualizované 31.1.2019 13:30

C	B	A
domáce kolo	domáce kolo	domáce kolo
školské kolo	školské kolo	školské kolo
krajské kolo	krajské kolo	krajské kolo
		celoštátne kolo
Zadania úloh domáceho kola vo formáte PDF: (uložiť ako …)

---

C-I-1
Dokážte, že pre ľubovoľné reálne číslo a platí nerovnosť

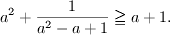
C-I-2
Nájdite najväčšie prirodzené číslo d, ktoré má tú vlastnosť, že pre ľubovoľné prirodzené číslo n je hodnota výrazu

deliteľná číslom d.

C-I-3
Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1 : 2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť

C-I-4
Nájdite všetky trojčleny P(x) = ax² + bx + c s celočíselnými koeficientmi a, b, c, pre ktoré platí P(1) < P(2) < P(3) a zároveň

C-I-5
V danom trojuholníku ABC zvoľme vnútri strany AC body K, M a vnútri strany BC body L, N tak, že

Ďalej označme E priesečník uhlopriečok lichobežníka ABLK, F priesečník uhlopriečok lichobežníka KLNM a G priesečník uhlopriečok lichobežníka ABNM. Dokážte, že body E, F a G ležia na ťažnici trojuholníka ABC z vrcholu C a určte pomer |GF|:|EF|.

C-I-6
a) Marienka rozmiestni do vrcholov pravidelného osemuholníka rôzne počty od jedného po osem cukríkov. Peter si potom môže vybrať, ktoré tri kôpky cukríkov dá Marienke, ostatné si ponechá. Jedinou podmienkou je, že tieto tri kôpky ležia vo vrcholoch rovnoramenného trojuholníka. Marienka chce rozmiestniť cukríky tak, aby ich dostala čo najviac, nech už Peter trojicu vrcholov vyberie akokoľvek. Koľko ich tak Marienka zaručene získa?
b) Rovnakú úlohu vyriešte aj pre pravidelný deväťuholník, do ktorého vrcholov rozmiestni Marienka 1 až 9 cukríkov. (Medzi rovnoramenné trojuholníky zaraďujeme aj trojuholníky rovnostranné.)

C-S-1

C-S-2

C-S-3

C-II-1

C-II-2

C-II-3

C-II-4

B-I-1

B-I-2

B-I-3

B-I-4

B-I-5

B-I-6

B-S-1

B-S-2

B-S-3

B-II-1

B-II-2

B-II-3

B-II-4

A-I-1
Pavol striedavo vpisuje krížiky a krúžky do políčok tabuľky (začína krížikom). Keď je tabuľka celá vyplnená, výsledné skóre spočíta ako rozdiel O — X, pričom O je celkový počet riadkov a stĺpcov obsahujúcich viac krúžkov ako krížikov a X je celkový počet riadkov a stĺpcov obsahujúcich viac krížikov ako krúžkov.

1. Dokážte, že pre tabuľku 2 x n bude výsledné skóre vždy 0.
2. Určte najvyššie možné skóre dosiahnuteľné pre tabuľku (2n + 1) x (2n + 1) v závislosti od n.

A-I-2
Dokážte, že ak je súčet dvoch daných reálnych čísel a, b väčší ako 2, má sústava nerovníc

nekonečne veľa riešení x v obore reálnych čísel.

A-I-3
V rovine sú dané dve zhodné kružnice s polomerom 1, ktoré majú vonkajší dotyk. Uvažujme pravouholník obsahujúci obe kružnice, ktorého každá strana sa dotýka aspoň jednej z nich. Určte najväčší a najmenší možný obsah takého pravouholníka.

A-I-4
Nájdite najväčšie prirodzené číslo n také, že hodnota súčtu

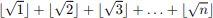
je prvočíslo. Zápis 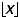označuje najväčšie celé číslo, ktoré nie je väčšie ako x.

A-I-5
V konvexnom štvoruholníku ABCD platí |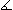ABC| = |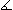ACD| a |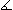ACB| = |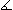ADC|.
Predpokladajme, že stred O kružnice opísanej trojuholníku BCD je rôzny od bodu A. Dokážte, že uhol OAC je pravý.

A-I-6
Nájdite najväčší možný počet prvkov množiny M celých čísel, ktorá má nasledujúcu vlastnosť: Z každej trojice rôznych čísel z M možno vybrať niektoré dve, ktorých súčet je mocninou čísla 2 s celočíselným exponentom.

A-S-1
Určte všetky reálne čísla p, pre ktoré má sústava nerovníc

aspoň jedno riešenie v obore reálnych čísel.

A-S-2
V trojuholníku ABC označme postupne S_b, S_c stredy strán AC, AB. Dokážte, že ak |AB|<|AC|, tak |∠BS_cC|<|∠BS_bC|.

A-S-3
Pavol striedavo vpisuje krížiky a krúžky do políčok tabuľky (začína krížikom). Keď je tabuľka celá vyplnená, výsledné skóre spočíta ako súčet X + O, pričom X je počet riadkov obsahujúcich viac krížikov ako krúžkov a O je počet stĺpcov obsahujúcich viac krúžkov ako krížikov. Určte najvyššie možné skóre dosiahnuteľné pre tabuľku (2n + 1) × (2n + 1) v závislosti od prirodzeného čísla n.

A-II-1

A-II-2

A-II-3

A-II-4

Uložiť

Uložiť

Uložiť